《2025年5年中考3年模拟八年级数学下册湘教版》

1. 图1是一顶圆锥形竹帽，图2是圆锥形竹帽的示意图，已知该圆锥的高$AO = 30\ cm$，底面半径$OB = 40\ cm$，
则$AB$的长为（ ）


A. 30 cm
B. 40 cm
C. 50 cm
D. 70 cm

答案： C $\because$ 圆锥的高 $AO = 30\ cm$，底面半径 $OB = 40\ cm$，
$\therefore AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{30^{2}+40^{2}} = 50(cm)$. 故选 C.

2.（2024湖南长沙宁乡期中）炭河古城作为我国首个周文化主题公园，备受大家追捧，如今已成为旅游热点. 下图是古城某个绿植拐角的平面图，为了不践踏绿植，需要避开“捷径$AC$”走横平竖直的路. 已知$AB = 6$米，$BC = 8$米，请问与捷径$AC$相比多走了（ ）

A. 2米
B. 3米
C. 4米
D. 5米

答案： C 在 $Rt\triangle ABC$ 中，$AB = 6$ 米，$BC = 8$ 米，由勾股定理得 $AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10$(米)，
$\because AB + BC - AC = 6 + 8 - 10 = 4$(米)，$\therefore$ 与捷径 $AC$ 相比多走了 4 米，故选 C.

3. 跨语文·古算诗（2024吉林中考）图①中有一首古算诗，根据诗中的描述可以计算出红莲所在位置的湖水深度，其示意图如图②，其中$AB = AB'$，$AB\perp B'C$于点$C$，$BC = 0.5$尺，$B'C = 2$尺. 设$AC$的长度为$x$尺，可列方程为__________.（M8201003）

答案： 答案 $x^{2}+2^{2}=(x + 0.5)^{2}$
解析 $AB' = AB=(x + 0.5)$ 尺，在 $Rt\triangle AB'C$ 中，由勾股定理得，$AC^{2}+B'C^{2}=AB'^{2}$，即 $x^{2}+2^{2}=(x + 0.5)^{2}$.

4. 情境题·国家安全 某日，南海舰队在中国南海例行训练，$A$舰艇突然发现在北偏西$30^{\circ}$方向上的$C$处有一可疑舰艇，$A$舰艇马上通知位于正东方向200海里处的$B$舰艇，$B$舰艇测得$C$处位于其北偏西$60^{\circ}$方向，请问此时两舰艇到$C$处的距离分别是多少？（M8201003）

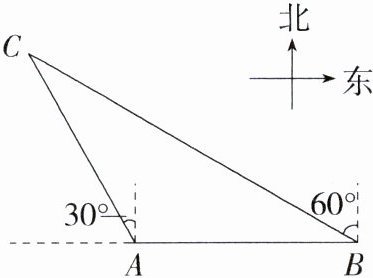
答案：
解析 如图，过点 $C$ 作 $CD\perp BA$ 交 $BA$ 的延长线于点 $D$，由题意可得，$\angle CAD = 60^{\circ}$，$\angle CBD = 30^{\circ}$，$\therefore \angle ACD = 30^{\circ}$，$\angle BCA=\angle CAD-\angle CBD = 60^{\circ}-30^{\circ}=30^{\circ}$，
$\therefore \angle BCA=\angle CBD$，$\therefore AC = AB = 200$ 海里.
在 $Rt\triangle CDA$ 中，$\because \angle ACD = 30^{\circ}$，
$\therefore AD=\frac{1}{2}AC = 100$ 海里.
根据勾股定理得 $CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{200^{2}-100^{2}} = 100\sqrt{3}$(海里)；
在 $Rt\triangle CDB$ 中，$\because \angle CBD = 30^{\circ}$，
$\therefore CB = 2CD = 200\sqrt{3}$ 海里.
故 $A$ 舰艇到 $C$ 处的距离为 200 海里，$B$ 舰艇到 $C$ 处的距离为 $200\sqrt{3}$ 海里.

5. 跨语文·古诗词（2024湖南永州道县月考）“儿童散学归来早，忙趁东风放纸鸢”. 又到了放风筝的最佳时节. 某校八年级（1）班的小明和小亮学习了“勾股定理”后，为了测得风筝的垂直高度$CE$（如图），他们进行了如下操作：①测得水平距离$BD$的长为15米；②根据手中剩余线的长度计算出风筝线$BC$的长为25米；③牵线放风筝的小明的身高（$AB$）为1.6米.
（1）求风筝的垂直高度$CE$.
（2）如果小明想风筝沿$CD$下降12米，那么他应该往回收线多少米？

答案：
解析
(1) 在 $Rt\triangle CDB$ 中，由勾股定理得，$CD^{2}=BC^{2}-BD^{2}=25^{2}-15^{2}=400$，
$\therefore CD = 20$(负值舍去)，
$\therefore CE = CD + DE = 20 + 1.6 = 21.6$(米).
答：风筝的垂直高度 $CE$ 为 21.6 米.
(2) 如图，根据题意，在 $CD$ 边上取一点 $M$，使得 $CM = 12$ 米，连接 $BM$，则 $DM = 8$ 米，

$\therefore BM=\sqrt{DM^{2}+BD^{2}}=\sqrt{8^{2}+15^{2}} = 17$(米)，
$\therefore BC - BM = 25 - 17 = 8$(米).
答：他应该往回收线 8 米.