《2025年5年中考3年模拟八年级数学下册湘教版》

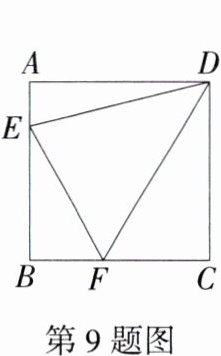
9. (2024湖南娄底期末)如图，在边长为4的正方形ABCD中，E、F分别是AB、BC上的点，连接DE、DF、EF，且∠EDF = 45°.若AE = 1，则EF的长为 ( )

A. 3$\sqrt{2}$
B. $\frac{8}{5}$
C. $\frac{8}{5}$$\sqrt{2}$
D. $\frac{17}{5}$

答案：
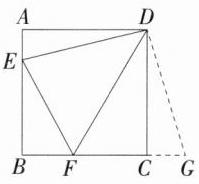
D 如图，延长BC，在BC的延长线上截取CG = AE = 1，连接DG，
∵四边形ABCD是正方形，
∴∠A = ∠BCD = ∠DCG = 90°，AD = CD，
∴△DAE≌△DCG(SAS)，
∴∠ADE = ∠CDG，DE = DG，
∵∠EDF = 45°，
∴∠ADE + ∠CDF = 45°，
∴∠CDG + ∠CDF = 45° = ∠FDG，
∴∠EDF = ∠FDG，
∴△DEF≌△DGF(SAS)，
∴EF = FG，设EF = FG = x，则FC = FG - CG = x - 1，BF = 5 - x，在Rt△BEF中，BE = 4 - 1 = 3，根据勾股定理得$BF^{2}+BE^{2}=EF^{2}，即(5 - x)^{2}+3^{2}=x^{2}$，
∴x = $\frac{17}{5}$，
∴EF的长为$\frac{17}{5}$.故选D.

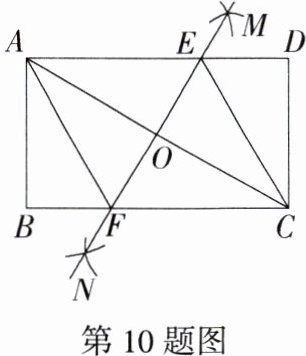
10. [新考向·尺规作图](2023山东日照一模)如图，在矩形ABCD中，AB＜BC，连接AC，分别以点A，C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧交于点M，N，连接MN分别交AD，BC，AC于点E，F，O，连接CE，AF.下列结论：①四边形AECF是菱形；②∠AFB = 2∠ACB；③AC·EF = CF·CD；④若AF平分∠BAC，则CF = $\sqrt{3}$AB.其中正确结论的个数是 ( )

A. 4
B. 3
C. 2
D. 1

答案： C 根据作图知EF垂直平分AC，
∴AO = CO，
∵AD//BC，
∴∠EAO = ∠FCO，在△AOE和△COF中，
$\begin{cases}\angle EAO=\angle FCO \\AO = CO \\\angle AOE=\angle COF = 90^{\circ}\end{cases}$
∴△AOE≌△COF(ASA)，
∴OE = OF，
∵OA = OC，AC⊥EF，
∴四边形AECF是菱形，故结论①正确；由结论①可得AF = CF，
∴∠FAC = ∠FCA，
∵∠AFB = ∠FAO + ∠ACB，
∴∠AFB = 2∠ACB，故结论②正确；
∵四边形AECF是菱形，
∴S_{四边形AECF}=CF\cdot CD=\frac{1}{2}AC\cdot EF，故结论③不正确；
∵四边形AECF为菱形，
∴∠FAC = ∠EAC，
∵AF平分∠BAC，
∴∠BAF = ∠FAC = ∠EAC=\frac{1}{3}×90° = 30°，
∴AF = 2BF，
∴AB = $\sqrt{3}BF$，
∵CF = AF，
∴CF = 2BF=\frac{2\sqrt{3}}{3}AB，故结论④不正确.故选C.

11. (2024重庆中考A卷)如果一个多边形的每一个外角都是40°，那么这个多边形的边数为________.

答案： 答案 9
解析 这个多边形的边数为360°÷40° = 9.

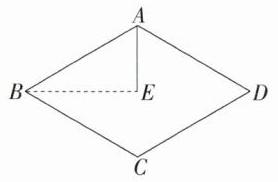
12. (2023陕西中考)若点E是菱形ABCD的对称中心，∠B = 56°，连接AE，则∠BAE的度数为________.

答案：
答案 62°
解析 如图，连接BE，
∵点E是菱形ABCD的对称中心，∠ABC = 56°，
∴点E是菱形ABCD的两条对角线的交点，
∴AE⊥BE，∠ABE=$\frac{1}{2}∠ABC = 28°$，
∴∠BAE = 90° - ∠ABE = 62°.

13. [新独家原创] 图1是某社区广场内的一个跷跷板的实物图，图2是其示意图.已知跷跷板的支点O是长板AB的中点，支柱高OC = 0.6 m.当长板的一端B着地时，长板的另一端到地面的高度AD为________.

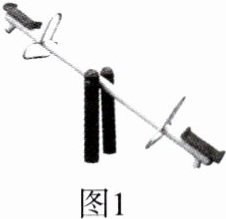
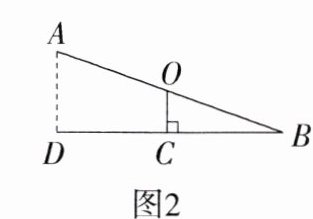
答案： 答案 1.2 m
解析 由题意可知，OC是△ABD的中位线，
∵OC = 0.6 m，
∴AD = 2OC = 1.2(m).

14. 如图，在矩形ABCD中，点E，F分别在BC，AD上，AF = EC，只需添加一个条件即可证明四边形AECF是菱形，这个条件可以是________(写出一个即可).

答案： 答案 AE = AF(答案不唯一)
解析 答案不唯一，如添加条件AE = AF.
∵四边形ABCD是矩形，
∴AF//CE，AF = EC，
∴四边形AECF是平行四边形，
∵AE = AF，
∴四边形AECF是菱形.

15. (2024湖南长沙岳麓月考)如图，在平行四边形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥AC交AD于点E.若AE = 4，DE = 2，DC = 2$\sqrt{5}$，则AC的长为________.

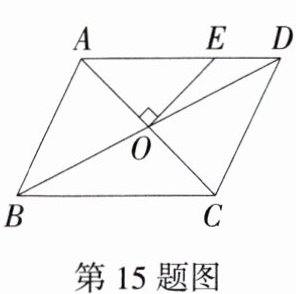
答案：
答案 4$\sqrt{2}$
解析 连接CE，
∵四边形ABCD是平行四边形，
∴AO = CO，
∵OE⊥AC，
∴OE垂直平分AC，
∴CE = AE = 4，
∵DE = 2，CD = 2$\sqrt{5}$，
∴$CE^{2}+DE^{2}=4^{2}+2^{2}=(2\sqrt{5})^{2}=CD^{2}$，
∴∠CED = ∠AEC = 90°，
∴△AEC是等腰直角三角形，
∴AC = 4$\sqrt{2}$.

16. 如图，E，F是正方形ABCD的对角线AC上的两点，AC = 8，AE = CF = 2，则四边形BEDF的周长是________.

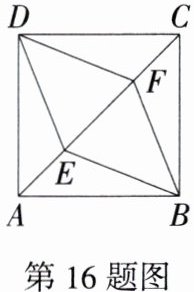
答案：
答案 8$\sqrt{5}$
解析 如图，连接BD交AC于点O，
∵四边形ABCD为正方形，
∴BD⊥AC，OD = OB = OA = OC = 4，
∵AE = CF = 2，
∴OA - AE = OC - CF，即OE = OF = 2，
∴四边形BEDF为平行四边形，
∵BD⊥EF，
∴四边形BEDF为菱形，
∴DE = DF = BE = BF，
由勾股定理得DE = $\sqrt{OD^{2}+OE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$，
∴四边形BEDF的周长 = 4DE = 4×2$\sqrt{5}$=8$\sqrt{5}$.

17. (2022黑龙江牡丹江、鸡西朝鲜族学校联合体中考)(6分)如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC与△DFE关于点O成中心对称，△ABC与△DEF的顶点均在格点上，请按要求完成下列各题.
(1)在图中画出点O的位置.
(2)将△ABC先向右平移4个单位长度，再向下平移2个单位长度，得到△A₁B₁C₁，请画出△A₁B₁C₁.

答案：
解析
(1)如图所示，点O即为所求.
(2)如图所示，$△A_{1}B_{1}C_{1}$即为所求.