《2025年5年中考3年模拟八年级数学下册湘教版》

1.(2024四川乐山中考)如图,下列各组条件中不能判定四边形ABCD为平行四边形的是 ( )

A.AB//DC,AD//BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB//DC,AD=BC

答案： D：
∵ 两组对边分别平行的四边形是平行四边形，
∴ A选项能判定这个四边形是平行四边形；
∵ 两组对边分别相等的四边形是平行四边形，
∴ B选项能判定这个四边形是平行四边形；
∵ 对角线互相平分的四边形是平行四边形，
∴ C选项能判定这个四边形是平行四边形；
∵ 一组对边平行，另一组对边相等的四边形，可能是平行四边形也可能是等腰梯形，
∴ D选项不能判定这个四边形是平行四边形。

2.下列各项是四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能够判定四边形ABCD是平行四边形的是 ( )
A.1∶2∶3∶4
B.2∶3∶2∶3
C.2∶2∶3∶4
D.1∶2∶2∶1

答案： B：A.
∵ ∠A，∠B，∠C，∠D 的度数之比为1∶2∶3∶4，
∴ 四边形ABCD的四个角都不相等，
∴ 四边形ABCD不是平行四边形，故选项A不符合题意；B.
∵ ∠A，∠B，∠C，∠D的度数之比为2∶3∶2∶3，
∴ 四边形ABCD的两组对角分别相等，
∴ 四边形ABCD是平行四边形，故选项B符合题意；C.
∵ ∠A，∠B，∠C，∠D的度数之比为2∶2∶3∶4，
∴ 四边形ABCD的两组对角不是分别相等的，
∴ 四边形ABCD不是平行四边形，故选项C不符合题意；D.
∵ ∠A，∠B，∠C，∠D的度数之比为1∶2∶2∶1，
∴ 四边形ABCD的两组对角不是分别相等的，
∴ 四边形ABCD不是平行四边形，故选项D不符合题意。故选B。

3.新独家原创 如图,下列四个条件:①AD//BC;②AB=CD;③∠A=∠C;④∠B=∠C,从中选一个,能使四边形ABCD为平行四边形的条件是________.(只填序号)(M8202002)

答案： 答案：①或②或③
解析：
∵ ∠A+∠D = 180°，
∴ AB//CD，①
∵ AD//BC，AB//CD，
∴ 四边形ABCD是平行四边形；②
∵ AB//CD，AB = CD，
∴ 四边形ABCD是平行四边形；③
∵ ∠A = ∠C，∠A+∠D = 180°，
∴ ∠C+∠D = 180°，
∴ AD//BC，
∵ AB//CD，
∴ 四边形ABCD是平行四边形；④由∠A+∠D = 180°，∠B = ∠C，不能得出四边形ABCD是平行四边形. 故答案为①或②或③。

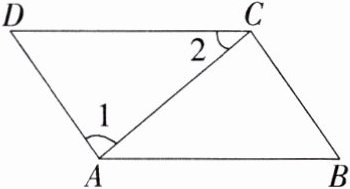
4.一题多解 如图,在四边形ABCD中,AB//DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数.
(2)求证:四边形ABCD是平行四边形.

答案： 解析：
（1）
∵ ∠D+∠2+∠1 = 180°，
∴ ∠D = 180° - ∠2 - ∠1 = 180° - 40° - 85° = 55°。
（2）证明：【证法一】
∵ AB//DC，
∴ ∠2+∠ACB+∠B = 180°，
∴ ∠ACB = 180° - ∠B - ∠2 = 180° - 55° - 40° = 85°，
∴ ∠ACB = ∠1，
∴ AD//BC，
∴ 四边形ABCD是平行四边形。
【证法二】
∵ AB//DC，
∴ ∠2 = ∠CAB，又
∵ ∠D = ∠B = 55°，AC = AC，
∴ △ACD≌△CAB（AAS），
∴ AB = CD，
∴ 四边形ABCD是平行四边形。

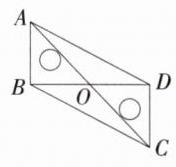
5.(2024贵州遵义二模)如图,将两个全等的直角三角尺(含30°角)的直角边重合,拼成如图1、图2所示的四边形ABCD.(M8202002)
(1)图1中四边形ABCD的形状为__________.
(2)连接AC,若直角三角尺的斜边长为12,请从图1、图2中选择一个图形,求对角线AC的长度.

答案：
解析：
（1）
∵ 两个直角三角尺全等，
∴ AB = CD，AD = BC，
∴ 四边形ABCD是平行四边形，故答案为平行四边形。
（2）（答案不唯一）选择图1. 连接AC交BD于点O，如图，
∵ ∠CBD = 30°，∠CDB = 90°，
∴ CD=$\frac{1}{2}$BC=$\frac{1}{2}$×12 = 6，
∴ BD = $\sqrt{BC^{2}-CD^{2}}$ = 6$\sqrt{3}$，
∵ 四边形ABCD是平行四边形，
∴ OD=$\frac{1}{2}$BD = 3$\sqrt{3}$，AC = 2OC，
∵ OC = $\sqrt{OD^{2}+DC^{2}}$ = 3$\sqrt{7}$，
∴ AC = 2OC = 6$\sqrt{7}$。

6.教材变式·P48练习T2 (2023浙江杭州中考)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.(M8202002)
(1)求证:四边形AECF是平行四边形.
(2)若△ABE的面积等于2,求△CFO的面积.

答案： 解析：
（1）证明：
∵ 四边形ABCD是平行四边形，
∴ AO = CO，BO = DO，
∵ BE = DF，
∴ EO = FO，
∴ 四边形AECF是平行四边形。
（2）
∵ BE = EF，
∴ $S_{\triangle AEF}=S_{\triangle ABE}=2$，
∵ 四边形AECF是平行四边形，
∴ $S_{\triangle CEF}=S_{\triangle AEF}=2$，EO = FO，
∴ $S_{\triangle CFO}=\frac{1}{2}S_{\triangle CEF}=1$。