第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.(2024湖南怀化月考)在平面直角坐标系中,点A(-3,4),点B是x轴上任意一点,则线段AB的最小值是 ( )
A.5
B.4
C.3
D.2
A.5
B.4
C.3
D.2
答案:
B:过点 A 作 AC⊥x 轴,垂足为点 C,图略,当点 B 与点 C 重合时,线段 AB 的长度最小,
∵ 点 A(-3,4),
∴ 线段 AB 的最小值为 4. 故选 B.
∵ 点 A(-3,4),
∴ 线段 AB 的最小值为 4. 故选 B.
2.(2022贵州铜仁中考)如图,在矩形ABCD中,A(-3,2),B(3,2),C(3,-1),则点D的坐标为 (M8203003) ( )

A.(-2,-1)
B.(4,-1)
C.(-3,-2)
D.(-3,-1)

A.(-2,-1)
B.(4,-1)
C.(-3,-2)
D.(-3,-1)
答案:
D:
∵A(-3,2),B(3,2),
∴AB = 6,AB//x 轴,
∵ 四边形 ABCD 是矩形,
∴CD = AB = 6,AB//CD,
∴CD//x 轴.
∵ 点 C 的坐标为(3,-1),
∴ 点 D 的坐标为(3 - 6,-1),即(-3,-1),故选 D.
∵A(-3,2),B(3,2),
∴AB = 6,AB//x 轴,
∵ 四边形 ABCD 是矩形,
∴CD = AB = 6,AB//CD,
∴CD//x 轴.
∵ 点 C 的坐标为(3,-1),
∴ 点 D 的坐标为(3 - 6,-1),即(-3,-1),故选 D.
3.(2024广西桂林期末)在平面直角坐标系中,A(1,3),B(1,-1),若点M在直线AB上,且AB = 2AM,则点M的坐标为 ( )
A.(1,1)
B.(1,1)或(1,5)
C.(1,-2)
D.(1,-2)或(1,5)
A.(1,1)
B.(1,1)或(1,5)
C.(1,-2)
D.(1,-2)或(1,5)
答案:
B:
∵A(1,3),B(1,-1),A、B 两点的横坐标相同,
∴AB = 4,AB 与 y 轴平行,又
∵AB = 2AM,点 M 在直线 AB 上,
∴ 点 M 的横坐标为 1,AM = 2,
∴ 点 M 的纵坐标为 3 + 2 = 5 或 3 - 2 = 1,
∴ 点 M 的坐标为(1,1)或(1,5),故选 B.
∵A(1,3),B(1,-1),A、B 两点的横坐标相同,
∴AB = 4,AB 与 y 轴平行,又
∵AB = 2AM,点 M 在直线 AB 上,
∴ 点 M 的横坐标为 1,AM = 2,
∴ 点 M 的纵坐标为 3 + 2 = 5 或 3 - 2 = 1,
∴ 点 M 的坐标为(1,1)或(1,5),故选 B.
4.新独家原创 如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(0,b),且a,b满足|a - 4| + $\sqrt{b - 3}$ = 0,则AB的长为________.
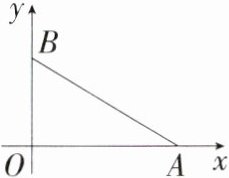

答案:
答案:5
解析:
∵|a - 4|+$\sqrt{b - 3}$ = 0,且|a - 4|≥0,$\sqrt{b - 3}$≥0,
∴a - 4 = 0,b - 3 = 0,
∴a = 4,b = 3,
∴OA = 4,OB = 3,在 Rt△AOB 中,AB = $\sqrt{OA^{2}+OB^{2}}$ = $\sqrt{4^{2}+3^{2}}$ = 5.
解析:
∵|a - 4|+$\sqrt{b - 3}$ = 0,且|a - 4|≥0,$\sqrt{b - 3}$≥0,
∴a - 4 = 0,b - 3 = 0,
∴a = 4,b = 3,
∴OA = 4,OB = 3,在 Rt△AOB 中,AB = $\sqrt{OA^{2}+OB^{2}}$ = $\sqrt{4^{2}+3^{2}}$ = 5.
5.教材变式·P93练习T2 如图,六边形ABCDEF在平面直角坐标系内.(M8203003)
(1)写出点A、B、C、D、E、F的坐标.
(2)求六边形ABCDEF的面积.
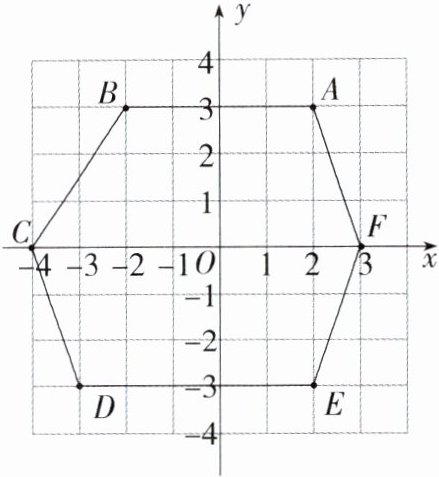
(1)写出点A、B、C、D、E、F的坐标.
(2)求六边形ABCDEF的面积.

答案:
解析:
(1) 由题图得 A(2,3)、B(-2,3)、C(-4,0)、D(-3,-3)、E(2,-3)、F(3,0).
(2)【解法一】六边形 ABCDEF 的面积 = 6×7 - $\frac{1}{2}$×2×3 - $\frac{1}{2}$×1×3 - $\frac{1}{2}$×1×3 - $\frac{1}{2}$×1×3 = 34.5.
【解法二】六边形 ABCDEF 的面积 = $\frac{1}{2}$×(4 + 7)×3 + $\frac{1}{2}$×(5 + 7)×3 = $\frac{33}{2}$ + $\frac{36}{2}$ = $\frac{69}{2}$ = 34.5.
(1) 由题图得 A(2,3)、B(-2,3)、C(-4,0)、D(-3,-3)、E(2,-3)、F(3,0).
(2)【解法一】六边形 ABCDEF 的面积 = 6×7 - $\frac{1}{2}$×2×3 - $\frac{1}{2}$×1×3 - $\frac{1}{2}$×1×3 - $\frac{1}{2}$×1×3 = 34.5.
【解法二】六边形 ABCDEF 的面积 = $\frac{1}{2}$×(4 + 7)×3 + $\frac{1}{2}$×(5 + 7)×3 = $\frac{33}{2}$ + $\frac{36}{2}$ = $\frac{69}{2}$ = 34.5.
6.(2024湖南邵阳期末,10,★★☆)如图,在平面直角坐标系xOy中,△AOB为等腰直角三角形,∠AOB = 90°,若点A的坐标为(2,3),则点B的坐标为 ( )
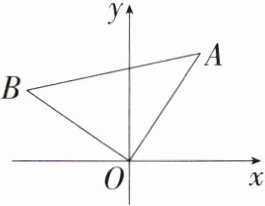
A.(-3,2)
B.(-2,3)
C.(3,2)
D.(2,-2)

A.(-3,2)
B.(-2,3)
C.(3,2)
D.(2,-2)
答案:
A:如图,分别过点 A,B 作 x 轴的垂线,垂足为点 M,N,则∠BNO = ∠AMO = 90°,
∵△AOB 是等腰直角三角形,
∴AO = BO,∠AOB = 90°,
∴∠AOM + ∠BON = 90°,又
∵AM⊥x 轴,
∴∠OAM + ∠AOM = 90°,
∴∠BON = ∠OAM,
∴△BON≌△OAM(AAS),
∴BN = OM,ON = AM.
∵A(2,3),
∴OM = 2,AM = 3,则 BN = 2,ON = 3,
∴B(-3,2). 故选 A.

A:如图,分别过点 A,B 作 x 轴的垂线,垂足为点 M,N,则∠BNO = ∠AMO = 90°,
∵△AOB 是等腰直角三角形,
∴AO = BO,∠AOB = 90°,
∴∠AOM + ∠BON = 90°,又
∵AM⊥x 轴,
∴∠OAM + ∠AOM = 90°,
∴∠BON = ∠OAM,
∴△BON≌△OAM(AAS),
∴BN = OM,ON = AM.
∵A(2,3),
∴OM = 2,AM = 3,则 BN = 2,ON = 3,
∴B(-3,2). 故选 A.

7.(2024湖南长沙期中,10,★★☆)如图,在平面直角坐标系中,点A,B,C的坐标分别为A(-4,0),B(4,0),C(0,3),连接AC,BC,若点M是直线BC上的一个动点,则当AM最短时,AM的长为 ( )

A.5
B.$\frac{24}{5}$
C.$\frac{12}{5}$
D.3

A.5
B.$\frac{24}{5}$
C.$\frac{12}{5}$
D.3
答案:
B:如图,
∵ 点 A,B,C 的坐标分别为 A(-4,0),B(4,0),C(0,3),
∴AB = 4 - (-4) = 8,OC = 3,在 Rt△OBC 中,BC = $\sqrt{OB^{2}+OC^{2}}$ = 5,过点 A 作 AD⊥BC 交 BC 的延长线于点 D,根据等面积法可得,$\frac{1}{2}$AB·OC = $\frac{1}{2}$BC·AD,
∴$\frac{1}{2}$×8×3 = $\frac{1}{2}$×5AD,
∴AD = $\frac{24}{5}$.
∵ 点 A 到直线 BC 的最短距离为垂线段 AD 的长度,
∴ 当 AM 最短时,点 M 与点 D 重合,即 AM = $\frac{24}{5}$,故选 B.
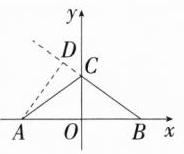
B:如图,
∵ 点 A,B,C 的坐标分别为 A(-4,0),B(4,0),C(0,3),
∴AB = 4 - (-4) = 8,OC = 3,在 Rt△OBC 中,BC = $\sqrt{OB^{2}+OC^{2}}$ = 5,过点 A 作 AD⊥BC 交 BC 的延长线于点 D,根据等面积法可得,$\frac{1}{2}$AB·OC = $\frac{1}{2}$BC·AD,
∴$\frac{1}{2}$×8×3 = $\frac{1}{2}$×5AD,
∴AD = $\frac{24}{5}$.
∵ 点 A 到直线 BC 的最短距离为垂线段 AD 的长度,
∴ 当 AM 最短时,点 M 与点 D 重合,即 AM = $\frac{24}{5}$,故选 B.

查看更多完整答案,请扫码查看


