第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
9.(2024湖南张家界模拟,7,★★☆)在平面直角坐标系$xOy$中,点$A$与点$A_1$关于$x$轴对称,点$A$与点$A_2$关于$y$轴对称.已知点$A_1(1,2)$,则点$A_2$的坐标是 ( )
A.$(-2,1)$
B.$(-2,-1)$
C.$(-1,2)$
D.$(-1,-2)$
A.$(-2,1)$
B.$(-2,-1)$
C.$(-1,2)$
D.$(-1,-2)$
答案:
D
∵点$A$与点$A_1$关于$x$轴对称,点$A_1(1,2)$,
∴点$A$的坐标为$(1,-2)$,
∵点$A$与点$A_2$关于$y$轴对称,
∴点$A_2$的坐标为$(-1,-2)$,故选D。
∵点$A$与点$A_1$关于$x$轴对称,点$A_1(1,2)$,
∴点$A$的坐标为$(1,-2)$,
∵点$A$与点$A_2$关于$y$轴对称,
∴点$A_2$的坐标为$(-1,-2)$,故选D。
10.(2021湖北荆州中考,5,★★☆)若点$P(a + 1,2 - 2a)$关于$x$轴对称的点在第四象限,则$a$的取值范围在数轴上表示为(M8203004) ( )
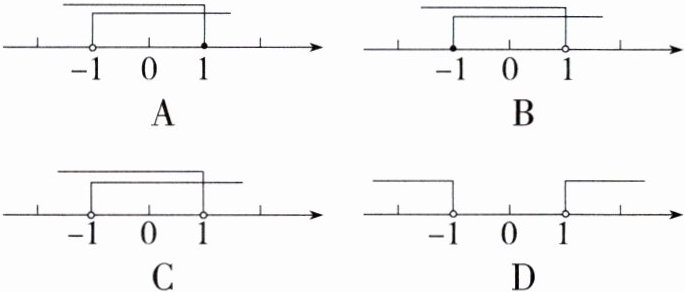

答案:
C
∵点$P(a + 1,2 - 2a)$关于$x$轴对称的点在第四象限,
∴点$P$在第一象限,
∴$\begin{cases}a + 1>0\\2 - 2a>0\end{cases}$,解得$-1 < a < 1$,
在数轴上的表示如图,故选C。
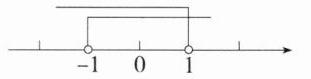
C
∵点$P(a + 1,2 - 2a)$关于$x$轴对称的点在第四象限,
∴点$P$在第一象限,
∴$\begin{cases}a + 1>0\\2 - 2a>0\end{cases}$,解得$-1 < a < 1$,
在数轴上的表示如图,故选C。

11.(2024山东济南高新区期末,20,★★☆)在$10×10$的网格中建立如图所示的直角坐标系,规定在网格内(包括边界)横、纵坐标都是整数的点称为格点,已知$\triangle ABC$的三个顶点都是格点,直线$m$经过点$(0,3)$且平行于$x$轴,直线$n$经过点$(-1,0)$且平行于$y$轴.
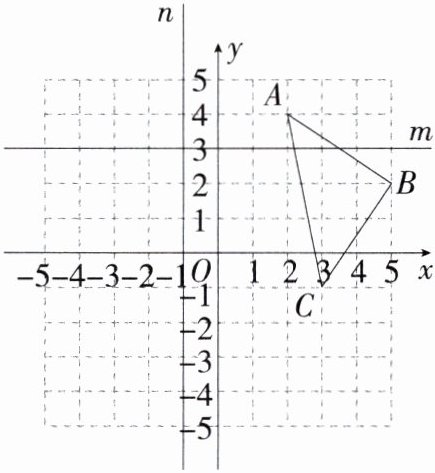
(1)$\triangle ABC$的顶点坐标分别是$A$(___,___),$B$(___,___),$C$(___,___).
(2)若$\triangle ABC$与$\triangle A'B'C'$关于$x$轴对称,$A,B,C$的对应点分别是$A',B',C'$,则$C'$(___,___).
(3)若点$D$是格点,且以点$A,B,C,D$为顶点的四边形是轴对称图形,则所有符合条件的点$D$坐标为________________.

(1)$\triangle ABC$的顶点坐标分别是$A$(___,___),$B$(___,___),$C$(___,___).
(2)若$\triangle ABC$与$\triangle A'B'C'$关于$x$轴对称,$A,B,C$的对应点分别是$A',B',C'$,则$C'$(___,___).
(3)若点$D$是格点,且以点$A,B,C,D$为顶点的四边形是轴对称图形,则所有符合条件的点$D$坐标为________________.
答案:
解析
(1)由题图可得,$A(2,4)$,$B(5,2)$,$C(3,-1)$。
(2)
∵点$C$的坐标是$(3,-1)$,且点$C$与点$C'$关于$x$轴对称,
∴$C'(3,1)$。
(3)
∵点$D$为格点,
∴当以点$A$,$B$,$C$,$D$为顶点的四边形是轴对称图形时,点$D$一定在线段$AC$的垂直平分线上,作图可知点$D$的坐标为$(0,1)$或$(-5,0)$,故答案为$(0,1)$或$(-5,0)$。
(1)由题图可得,$A(2,4)$,$B(5,2)$,$C(3,-1)$。
(2)
∵点$C$的坐标是$(3,-1)$,且点$C$与点$C'$关于$x$轴对称,
∴$C'(3,1)$。
(3)
∵点$D$为格点,
∴当以点$A$,$B$,$C$,$D$为顶点的四边形是轴对称图形时,点$D$一定在线段$AC$的垂直平分线上,作图可知点$D$的坐标为$(0,1)$或$(-5,0)$,故答案为$(0,1)$或$(-5,0)$。
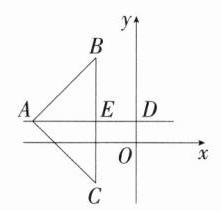
12.(2024河北邢台期末,23,★★☆)如图,在平面直角坐标系中,过点$A$作$AD\perp y$轴,垂足为$D$,点$B$关于直线$AD$的对称点为点$C$,连接$AC,AB,BC$,已知$AD = 10$,$OD = 2$.
(1)点$A$的坐标为________.
(2)若点$C(-4,-4)$,请判断$\triangle ABC$的形状,并说明理由.
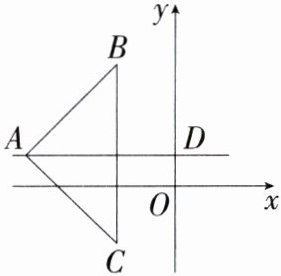
(1)点$A$的坐标为________.
(2)若点$C(-4,-4)$,请判断$\triangle ABC$的形状,并说明理由.

答案:
解析
(1)
∵$AD\perp y$轴,$AD = 10$,$OD = 2$,
∴点$A$的坐标为$(-10,2)$。故答案为$(-10,2)$。
(2)$\triangle ABC$为等腰直角三角形。
理由:如图,设直线$AD$与$BC$交于点$E$。
∵点$B$关于直线$AD$的对称点为点$C$,
∴$BC\perp AD$,$BE = CE$。
∴$AB = AC$。
∵点$C$的坐标为$(-4,-4)$,
∴点$E$的坐标为$(-4,2)$,
又
∵点$A$的坐标为$(-10,2)$,
∴$AE = CE = 6$,
∴$\angle CAE = \angle C = 45^{\circ}$,
∵$AB = AC$,
∴$\angle B = \angle C = 45^{\circ}$,
∴$\angle BAC = 90^{\circ}$,
∴$\triangle ABC$为等腰直角三角形。
解析
(1)
∵$AD\perp y$轴,$AD = 10$,$OD = 2$,
∴点$A$的坐标为$(-10,2)$。故答案为$(-10,2)$。
(2)$\triangle ABC$为等腰直角三角形。
理由:如图,设直线$AD$与$BC$交于点$E$。
∵点$B$关于直线$AD$的对称点为点$C$,
∴$BC\perp AD$,$BE = CE$。
∴$AB = AC$。
∵点$C$的坐标为$(-4,-4)$,
∴点$E$的坐标为$(-4,2)$,
又
∵点$A$的坐标为$(-10,2)$,
∴$AE = CE = 6$,
∴$\angle CAE = \angle C = 45^{\circ}$,
∵$AB = AC$,
∴$\angle B = \angle C = 45^{\circ}$,
∴$\angle BAC = 90^{\circ}$,
∴$\triangle ABC$为等腰直角三角形。

13.(2024湖南衡阳期末,23,★★☆)点$P(a,b)$是平面直角坐标系$xOy$内一点,点$P$的轴变换定义:当$|a|>|b|$时,作点$P$关于$x$轴对称;当$|a|\leq|b|$时,作点$P$关于$y$轴对称.根据定义,解决下列问题:
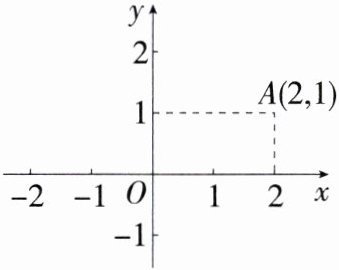
如图,平面直角坐标系中,点$A$的坐标为$(2,1)$,点$B$的坐标为$(-1,m)$,其中$m < - 1$,点$A,B$轴变换后的对应点是点$A',B'$.
(1)求$A',B'$的坐标.
(2)若$A'B = AB'$,求$m$的值.
如图,平面直角坐标系中,点$A$的坐标为$(2,1)$,点$B$的坐标为$(-1,m)$,其中$m < - 1$,点$A,B$轴变换后的对应点是点$A',B'$.
(1)求$A',B'$的坐标.
(2)若$A'B = AB'$,求$m$的值.

答案:
解析
(1)
∵点$A(2,1)$,且$\vert2\vert>\vert1\vert$,
∴点$A(2,1)$关于$x$轴对称的点$A'$的坐标是$(2,-1)$,
∵点$B$的坐标为$(-1,m)$,其中$m < -1$,即$\vert -1\vert<\vert m\vert$,
∴点$B(-1,m)$关于$y$轴对称的点$B'$的坐标是$(1,m)$,
∴$A'(2,-1)$,$B'(1,m)$。
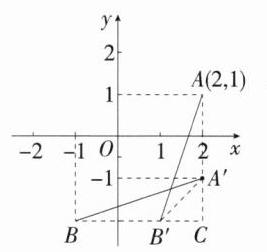
(2)如图,由
(1)可得$A'(2,-1)$,$B'(1,m)$,延长$AA'$、$BB'$相交于点$C$,则$C(2,m)$。
由对称可知,$AA' = BB' = 2$,
又
∵$A'B = AB'$,$A'B' = A'B'$,
∴$\triangle AA'B'\cong\triangle BB'A'(SSS)$,
∴$\angle B'AA' = \angle B'BA'$,
∵$A'B = AB'$,$\angle B'AA' = \angle B'BA'$,$\angle C = \angle C = 90^{\circ}$,
∴$\triangle AB'C\cong\triangle BA'C(AAS)$,
∴$A'C = B'C$,即$-1 - m = 2 - 1$,
∴$m = -2$。
解析
(1)
∵点$A(2,1)$,且$\vert2\vert>\vert1\vert$,
∴点$A(2,1)$关于$x$轴对称的点$A'$的坐标是$(2,-1)$,
∵点$B$的坐标为$(-1,m)$,其中$m < -1$,即$\vert -1\vert<\vert m\vert$,
∴点$B(-1,m)$关于$y$轴对称的点$B'$的坐标是$(1,m)$,
∴$A'(2,-1)$,$B'(1,m)$。
(2)如图,由
(1)可得$A'(2,-1)$,$B'(1,m)$,延长$AA'$、$BB'$相交于点$C$,则$C(2,m)$。
由对称可知,$AA' = BB' = 2$,
又
∵$A'B = AB'$,$A'B' = A'B'$,
∴$\triangle AA'B'\cong\triangle BB'A'(SSS)$,
∴$\angle B'AA' = \angle B'BA'$,
∵$A'B = AB'$,$\angle B'AA' = \angle B'BA'$,$\angle C = \angle C = 90^{\circ}$,
∴$\triangle AB'C\cong\triangle BA'C(AAS)$,
∴$A'C = B'C$,即$-1 - m = 2 - 1$,
∴$m = -2$。

查看更多完整答案,请扫码查看


