《2025年5年中考3年模拟八年级数学下册湘教版》

11.(2024四川自贡中考)凸七边形的内角和是______°.

答案： 900\n解析：凸七边形的内角和为$180^{\circ}\times(7 - 2)=900^{\circ}$。

12.新考向·开放性试题 (2022黑龙江齐齐哈尔中考)在四边形ABCD中,AC⊥BD,垂足为O,AB//CD,要使四边形ABCD为菱形,应添加的条件是________.(只需写出一个条件即可)

答案： AB = CD（答案不唯一）\n解析：添加的条件可以是$AB = CD$（答案不唯一），理由如下：$\because AB// CD$，$AB = CD$，$\therefore$四边形$ABCD$是平行四边形，$\because AC\perp BD$，$\therefore$平行四边形$ABCD$是菱形。

13.(2024江苏淮安一模)如图,将边长为1的6个小正方形拼成长方形后放置在Rt△POQ的边上,长方形的两个顶点分别落在边OP,OQ上,设C,D为小正方形的顶点,连接OC,恰好经过小正方形的顶点D,则OC的长为________.

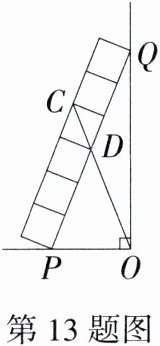
答案： $3+\sqrt{2}$   解析：由题意得$CD=\sqrt{1^{2}+1^{2}}=\sqrt{2}$，$PQ = 6$，$\because\angle POQ = 90^{\circ}$，$PD = QD$，$\therefore DO=\frac{1}{2}PQ = 3$，$\therefore CO = DO + CD = 3+\sqrt{2}$。

14.(2024湖南怀化期中)如图,□ABCD的周长是24 cm,对角线AC、BD相交于点O,且EO⊥BD,则△ABE的周长为________.

答案： 12 cm\n解析：$\because$四边形$ABCD$是平行四边形，$\therefore OB = OD$，$\because OE\perp BD$，$\therefore OE$垂直平分$BD$，$\therefore BE = DE$，$\because\square ABCD$的周长是$24\ cm$，$\therefore\triangle ABE$的周长$=AB + AE+BE = AB + AE + DE = AB + AD=\frac{1}{2}\times24 = 12(cm)$。

15.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB = 3,则BC的长为________.

答案： $\sqrt{3}$\n解析：$\because$四边形$AECF$是菱形，$\therefore\angle FCO=\angle ECO$，由折叠的性质可知$\angle ECO=\angle BCE$，$\because\angle FCO+\angle ECO+\angle BCE = 90^{\circ}$，$\therefore\angle FCO=\angle ECO=\angle BCE = 30^{\circ}$，在$Rt\triangle EBC$中，$EC = 2EB$，又$\because EC = AE$，$AB = AE + EB = 3$，$\therefore EB = 1$，$EC = 2$，$\therefore BC=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。

16.跨艺术·立体画 (2022山东青岛中考)图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果.图②是一个菱形,将其截去一个边长为原来一半的菱形后得到图③,用图③镶嵌得到图④,将图④着色后,再次镶嵌便得到图①,则图④中∠ABC的度数是________.

答案：
60°
解析：如图，$\because\angle BAD=\angle BAE=\angle DAE$，$\angle BAD+\angle BAE+\angle DAE = 360^{\circ}$，$\therefore\angle BAD=\angle BAE=\angle DAE = 120^{\circ}$，$\because BC// AD$，$\therefore\angle ABC = 180^{\circ}-120^{\circ}=60^{\circ}$。

17.(2023广西中考)如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为________.

答案：
$\sqrt{2}$    解析：如图所示，连接$AE$，$\because M$，$N$分别是$EF$，$AF$的中点，$\therefore MN$是$\triangle AEF$的中位线，$\therefore MN=\frac{1}{2}AE$，$\because$四边形$ABCD$是正方形，$\therefore\angle B = 90^{\circ}$，$\therefore AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{4 + BE^{2}}$，$\therefore$当$BE$的值最大时，$AE$的值最大，此时$MN$的值最大，$\because$点$E$是$BC$上的动点，$\therefore$当点$E$和点$C$重合时，$BE$的值最大，此时$AE=\sqrt{4 + 2^{2}}=2\sqrt{2}$，$\therefore MN=\frac{1}{2}AE=\sqrt{2}$，$\therefore MN$的最大值为$\sqrt{2}$。

18.(2024湖南郴州模拟)如图,在菱形ABCD中,AB = 4,∠BAD = 60°,对角线AC与BD相交于点O,将边AD沿AC向右平移得到FE,连接DE.当点F是OA的中点时,四边形ADEF的面积为________.

答案： 2$\sqrt{3}$\n解析：$\because$四边形$ABCD$是菱形，$AB = 4$，$\therefore AD = AB = 4$，$OB = OD$，$OA = OC$，$AC\perp BD$，$\therefore\angle AOD = 90^{\circ}$，$\because\angle BAD = 60^{\circ}$，$\therefore\triangle ABD$是等边三角形，$\therefore BD = AB = 4$，$\therefore OD = 2$，$\therefore OA=\sqrt{AD^{2}-OD^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$，$\because$点$F$是$OA$的中点，$\therefore AF=\frac{1}{2}OA=\sqrt{3}$，由平移的性质得$EF// AD$，$EF = AD$，$\therefore$四边形$ADEF$是平行四边形，$\therefore S_{\square ADEF}=AF\cdot OD=\sqrt{3}\times2 = 2\sqrt{3}$。

19.[答案含评分细则](2024湖南娄底月考)(8分)如图,四边形ABCD中,∠ACB = 90°,AB = 15,BC = 9,AD = 5,DC = 13,求四边形ABCD的面积.

答案： 解析：\n在$Rt\triangle ACB$中，$\angle ACB = 90^{\circ}$，$AB = 15$，$BC = 9$，$\therefore AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{15^{2}-9^{2}}=12$。$\cdots\cdots2$分\n$\because AD = 5$，$CD = 13$，$\therefore AD^{2}+AC^{2}=5^{2}+12^{2}=169 = 13^{2}=CD^{2}$，$\therefore\triangle ACD$是直角三角形，且$\angle CAD = 90^{\circ}$，$\cdots\cdots4$分\n$\therefore S_{\triangle ACD}=\frac{1}{2}AD\cdot AC=\frac{1}{2}\times5\times12 = 30$，$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}\times12\times9 = 54$，$\therefore S_{四边形 ABCD}=S_{\triangle ACD}+S_{\triangle ABC}=30 + 54 = 84$。$\cdots\cdots8$分