《2025年5年中考3年模拟八年级数学下册湘教版》

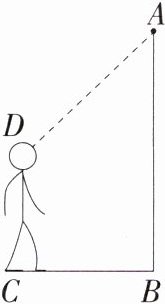
6.（2024湖南邵阳期中，9，★★☆）如图，某自动感应门的正上方$A$处装有一个感应器，它离地面的高度$AB$为2.5米，一名学生站在$C$处时，感应门自动打开了，此时这名学生离感应门的距离$BC$为1.2米，头顶离感应器的距离$AD$为1.5米，则这名学生的身高$CD$为（M8201003）（ ）

A. 0.9米
B. 1.3米
C. 1.5米
D. 1.6米

答案：
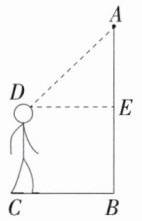
D 过点 $D$ 作 $DE\perp AB$ 于 $E$，如图所示，
则 $CD = BE$，$DE = BC = 1.2$ 米，
在 $Rt\triangle ADE$ 中，$AD = 1.5$ 米，
由勾股定理得，$AE=\sqrt{AD^{2}-DE^{2}}=\sqrt{1.5^{2}-1.2^{2}} = 0.9$(米)，
$\therefore BE = AB - AE = 2.5 - 0.9 = 1.6$(米)，
$\therefore CD = BE = 1.6$ 米，故选 D.

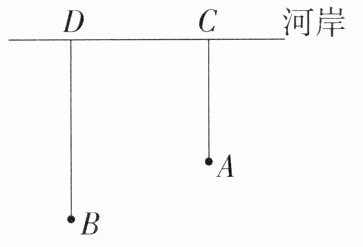
7.（2023山东青岛实验学校期中，7，★★☆）如图，牧童在$A$处放牛，牧童家在$B$处，$A$、$B$两处到河岸$DC$的距离$AC$、$BD$分别为500 m、700 m，且$C$、$D$两处的距离为500 m，天黑前牧童将牛从$A$处牵到河边饮完水再回家，那么牧童要走的路程最少为（ ）


A. 1 000 m
B. 1 200 m
C. 1 300 m
D. 1 700 m

答案：
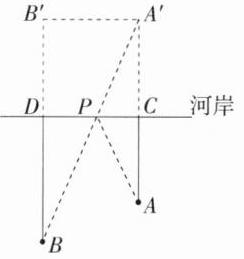
C 如图，作 $A$ 点关于河岸 $CD$ 的对称点 $A'$，连接 $BA'$ 交河岸 $CD$ 于 $P$，连接 $PA$，过 $A'$ 作 $A'B'\perp BD$ 交 $BD$ 的延长线于 $B'$，则 $PB + PA = PB + PA' = BA'$，将牛牵到河边的 $P$ 处饮水，此时牧童所走的路程最短.
易知 $B'D = A'C = AC = 500\ m$，$\therefore BB' = BD + B'D = 700 + 500 = 1200(m)$，$\because A'B' = CD = 500\ m$，
$\therefore BA'=\sqrt{BB'^{2}+A'B'^{2}}=\sqrt{1200^{2}+500^{2}} = 1300(m)$.
故牧童要走的路程至少为 1300 m，故选 C.

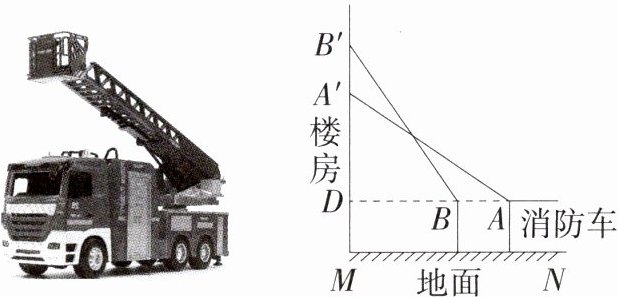
8.（2024湖南娄底期中改编，22，★★☆）如图，已知云梯最多只能伸长到50米（即$AA' = BB' = 50$米），消防车高3.4米，救人时云梯伸长至最长，在从33.4米（即$A'M = 33.4$米）高的$A$处救完人后，还要从51.4米（即$B'M = 51.4$米）高的$B$处救人，这时消防车从$A$处向着火的楼房靠近的距离$AB$为________米.

答案： 答案 26
解析 由题意可知，$DM = 3.4$ 米，$AA' = BB' = 50$ 米，$A'M = 33.4$ 米，$B'M = 51.4$ 米，$AD\perp B'M$，点 $A$、$B$、$D$ 三点共线，$\therefore A'D = A'M - DM = 33.4 - 3.4 = 30$(米)，$B'D = B'M - DM = 51.4 - 3.4 = 48$(米)，
在 $Rt\triangle AA'D$ 中，由勾股定理得 $AD=\sqrt{AA'^{2}-A'D^{2}}=\sqrt{50^{2}-30^{2}} = 40$(米)，
在 $Rt\triangle BB'D$ 中，由勾股定理得 $BD=\sqrt{BB'^{2}-B'D^{2}}=\sqrt{50^{2}-48^{2}} = 14$(米)，
$\therefore AB = AD - BD = 40 - 14 = 26$(米).
故这时消防车从 $A$ 处向着火的楼房靠近的距离 $AB$ 为 26 米.

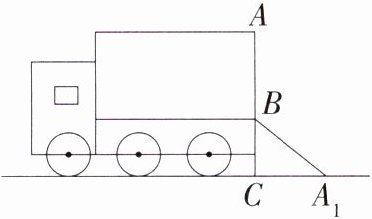
1. 单勾股 如图，货车车高$AC = 4\ m$，卸货时后面的挡板$AB$的顶部$A$折落在地面$A_1$处，已知点$A$、$B$、$C$在一条直线上，$AC\perp A_1C$，经过测量得$A_1C = 2\ m$，则$BC =$________.

答案： 答案 $1.5\ m$
解析 由题意得，$AB = A_{1}B$，$\angle BCA_{1}=90^{\circ}$，设 $BC = x\ m$，则 $A_{1}B = AB=(4 - x)\ m$，在 $Rt\triangle A_{1}BC$ 中，$A_{1}C^{2}+BC^{2}=A_{1}B^{2}$，即 $2^{2}+x^{2}=(4 - x)^{2}$，解得 $x = 1.5$.$\therefore BC = 1.5\ m$.

2. 双勾股 如图，某段高速公路上有$A$、$B$两点相距10 km，$C$、$D$为两村庄，已知$DA\perp AB$于点$A$，$CB\perp AB$于点$B$，$DA = 4\ km$，$CB = 6\ km$. 现在要在$AB$上建一个服务站$E$，使得$C$、$D$两村庄到服务站$E$的距离相等，则$EA$的长是________.

答案： 答案 $6\ km$
解析 设 $BE = x\ km$，则 $AE=(10 - x)\ km$，
在 $Rt\triangle ADE$ 中，$DE^{2}=AD^{2}+AE^{2}=4^{2}+(10 - x)^{2}$，
在 $Rt\triangle BCE$ 中，$CE^{2}=BC^{2}+BE^{2}=6^{2}+x^{2}$，由题意可知 $DE = CE$，$\therefore 6^{2}+x^{2}=4^{2}+(10 - x)^{2}$，解得 $x = 4$，$\therefore BE = 4\ km$，$\therefore EA = 10 - 4 = 6(km)$.

3. 双勾股 如图，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$CD\perp AB$于点$D$，$AD = 4$，$BD = 9$，则$CA =$________，$BC =$________.

答案： 答案 $2\sqrt{13}$；$3\sqrt{13}$
解析 设 $CD = x$，则 $AC^{2}=x^{2}+4^{2}$，$BC^{2}=x^{2}+9^{2}$，在 $Rt\triangle ABC$ 中，$AC^{2}+BC^{2}=x^{2}+16+x^{2}+81 = AB^{2}=13^{2}$，解得 $x = 6$，$\therefore AC=\sqrt{6^{2}+4^{2}} = 2\sqrt{13}$，$BC=\sqrt{6^{2}+9^{2}} = 3\sqrt{13}$.