第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1. [新独家原创] 风铃,又称铁马,古称“铎”,常见于中国传统建筑屋檐下.如图所示的是六角形风铃,其底部可抽象看成正六边形,则正六边形的内角和是 ( )

A. 900°
B. 720°
C. 540°
D. 360°

A. 900°
B. 720°
C. 540°
D. 360°
答案:
B 正六边形的内角和是(6 - 2)×180° = 720°.
2. 我国民间建筑装饰图案中蕴含着丰富的数学之美.下列图案中既是轴对称图形又是中心对称图形的是(M8202003) ( )
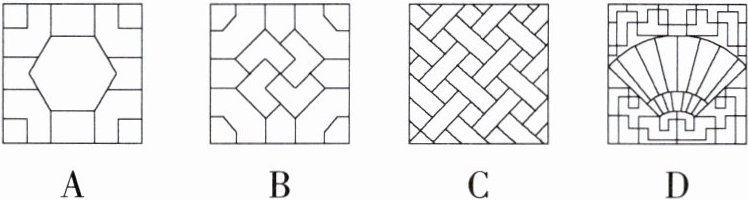

答案:
A A.该图案既是轴对称图形,也是中心对称图形;B.该图案不是轴对称图形,是中心对称图形;C.该图案既不是轴对称图形,也不是中心对称图形;D.该图案是轴对称图形,但不是中心对称图形.故选A.
3. (2024贵州中考)如图,□ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
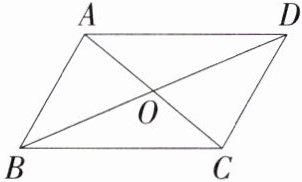
A. AB = BC
B. AD = BC
C. OA = OB
D. AC⊥BD

A. AB = BC
B. AD = BC
C. OA = OB
D. AC⊥BD
答案:
B
∵平行四边形的对边相等,
∴AD = BC.故选B.
∵平行四边形的对边相等,
∴AD = BC.故选B.
4. 如图,菱形ABCD的一边中点M到对角线的交点O的距离为3 cm,则菱形ABCD的周长为 ( )
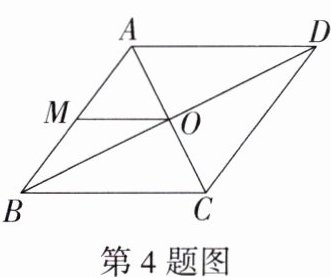
A. 10 cm
B. 12 cm
C. 16 cm
D. 24 cm

A. 10 cm
B. 12 cm
C. 16 cm
D. 24 cm
答案:
D
∵四边形ABCD是菱形,
∴AB = AD = CD = BC,BO = OD,又
∵点M是AB的中点,
∴OM是△BAD的中位线,
∴AD = 2OM = 6 cm,
∴菱形ABCD的周长 = 4×6 = 24(cm),故选D.
∵四边形ABCD是菱形,
∴AB = AD = CD = BC,BO = OD,又
∵点M是AB的中点,
∴OM是△BAD的中位线,
∴AD = 2OM = 6 cm,
∴菱形ABCD的周长 = 4×6 = 24(cm),故选D.
5. (2024湖南常德安乡一模)两个矩形的位置如图所示,若∠1 = α,则∠2 = ( )
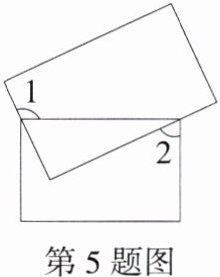
A. α - 90°
B. 180° - α
C. α - 45°
D. 270° - α

A. α - 90°
B. 180° - α
C. α - 45°
D. 270° - α
答案:
B 如图,
∵四边形ABCD和四边形EFGH都是矩形,
∴∠B = ∠EHG = 90°,
∵∠1是△EBH的一个外角,
∴∠3 = ∠1 - ∠B = α - 90°,
∴∠2 = ∠EHG - ∠3 = 90° - (α - 90°) = 180° - α.故选B.
B 如图,
∵四边形ABCD和四边形EFGH都是矩形,
∴∠B = ∠EHG = 90°,
∵∠1是△EBH的一个外角,
∴∠3 = ∠1 - ∠B = α - 90°,
∴∠2 = ∠EHG - ∠3 = 90° - (α - 90°) = 180° - α.故选B.

6. (2023内蒙古通辽中考)如图,用平移方法说明平行四边形的面积公式S = ah时,若△ABE平移到△DCF,a = 4,h = 3,则△ABE的平移距离为 ( )
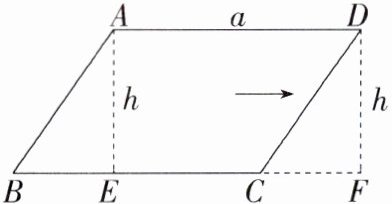
A. 3
B. 4
C. 5
D. 12

A. 3
B. 4
C. 5
D. 12
答案:
B
∵四边形ABCD是平行四边形,
∴AD//EF,BC = AD = a,
∵AE⊥BC,DF⊥BC,
∴AE//DF,
∴四边形AEFD是矩形,由平移的性质得BE = CF,
∴EF = BC = a = 4,
∴△ABE的平移距离为4.故选B.
∵四边形ABCD是平行四边形,
∴AD//EF,BC = AD = a,
∵AE⊥BC,DF⊥BC,
∴AE//DF,
∴四边形AEFD是矩形,由平移的性质得BE = CF,
∴EF = BC = a = 4,
∴△ABE的平移距离为4.故选B.
7. (2024湖南长沙一中教育集团期中)如图,四边形ABCD为平行四边形,延长AD到E,使DE = AD,连接EB,EC,DB,添加一个条件,不一定能使四边形DBCE成为矩形的是 ( )
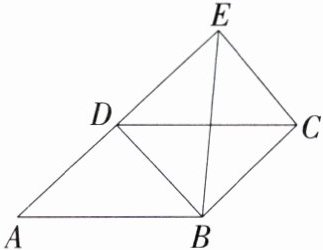
A. AB = BE
B. ∠ADB = 90°
C. BE⊥DC
D. CE⊥DE

A. AB = BE
B. ∠ADB = 90°
C. BE⊥DC
D. CE⊥DE
答案:
C
∵四边形ABCD为平行四边形,
∴AD//BC,AD = BC,
∵AD = DE,
∴DE = BC,
∴四边形DBCE为平行四边形.
∵AB = BE,AB = CD,
∴BE = CD,
∴□DBCE为矩形,故选项A不符合题意;
∵∠ADB = 90°,
∴∠EDB = 90°,
∴□DBCE为矩形,故选项B不符合题意;对角线互相垂直的平行四边形为菱形,不一定为矩形,故选项C符合题意;
∵CE⊥DE,
∴∠CED = 90°,
∴□DBCE为矩形,故选项D不符合题意.故选C.
∵四边形ABCD为平行四边形,
∴AD//BC,AD = BC,
∵AD = DE,
∴DE = BC,
∴四边形DBCE为平行四边形.
∵AB = BE,AB = CD,
∴BE = CD,
∴□DBCE为矩形,故选项A不符合题意;
∵∠ADB = 90°,
∴∠EDB = 90°,
∴□DBCE为矩形,故选项B不符合题意;对角线互相垂直的平行四边形为菱形,不一定为矩形,故选项C符合题意;
∵CE⊥DE,
∴∠CED = 90°,
∴□DBCE为矩形,故选项D不符合题意.故选C.
8. [和差法求面积] 如图,在四边形ABCD中,∠ABC = 90°,AB = BC = 2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,点D到EF的距离为0.5,则△BEF的面积为 ( )
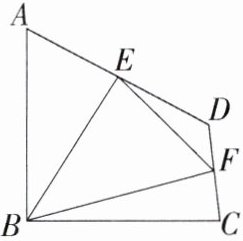
A. 2
B. $\frac{9}{4}$
C. $\frac{5}{2}$
D. 3

A. 2
B. $\frac{9}{4}$
C. $\frac{5}{2}$
D. 3
答案:
C 如图,连接AC,BD,则$S_{△ABC} $= $\frac{1}{2}BC\cdot AB=\frac{1}{2}\times2\sqrt{2}\times2\sqrt{2}=4$.
∵四边形ABCD的面积为6,
∴$S_{△ADC} = 6 - 4 = 2$,
∵E、F分别是AD、CD的中点,
∴AE = DE,DF = CF,
∴$S_{△ABE}+S_{△BCF}$=$\frac{1}{2}S_{四边形ABCD}=3,S_{△EDF}=\frac{1}{4}S_{△ADC}=\frac{1}{2}$,
∴$S_{△BEF}=S_{四边形ABCD}-S_{△ABE}-S_{△BCF}-S_{△FED}=6 - 3-\frac{1}{2}=\frac{5}{2}$,故选C.
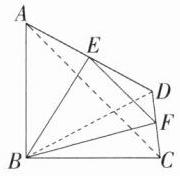
C 如图,连接AC,BD,则$S_{△ABC} $= $\frac{1}{2}BC\cdot AB=\frac{1}{2}\times2\sqrt{2}\times2\sqrt{2}=4$.
∵四边形ABCD的面积为6,
∴$S_{△ADC} = 6 - 4 = 2$,
∵E、F分别是AD、CD的中点,
∴AE = DE,DF = CF,
∴$S_{△ABE}+S_{△BCF}$=$\frac{1}{2}S_{四边形ABCD}=3,S_{△EDF}=\frac{1}{4}S_{△ADC}=\frac{1}{2}$,
∴$S_{△BEF}=S_{四边形ABCD}-S_{△ABE}-S_{△BCF}-S_{△FED}=6 - 3-\frac{1}{2}=\frac{5}{2}$,故选C.

查看更多完整答案,请扫码查看


