《2025年5年中考3年模拟八年级数学下册湘教版》

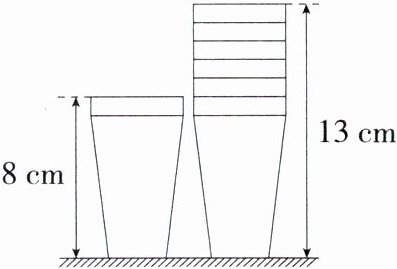
1.（2024湖南永州冷水滩模拟）下图是1个纸杯及6个纸杯叠放在一起的示意图.小红了解到叠放在一起的纸杯的总高度随纸杯数量的变化满足一次函数关系,她将50个同样的纸杯叠放在一起,则这50个纸杯的总高度约为（ ）

A.50 cm
B.56 cm
C.57 cm
D.58 cm

答案： **C**
设叠放在一起的纸杯的总高度$y(\text{cm})$与纸杯数量$x$(个)之间的函数关系式为$y = kx + b(k\neq0)$，将$(1,8)$，$(6,13)$代入$y = kx + b$得$\begin{cases}k + b = 8\\6k + b = 13\end{cases}$，解得$\begin{cases}k = 1\\b = 7\end{cases}$。
$\therefore$叠放在一起的纸杯的总高度$y(\text{cm})$与纸杯数量$x$(个)之间的函数关系式为$y = x + 7$。当$x = 50$时，$y = 1\times50 + 7 = 57$，$\therefore$这$50$个纸杯的总高度约为$57\text{ cm}$。故选 C。

2.（跨物理·沸点测定 新独家原创）沸点测定法是一种常用的物理实验方法,用于测定液体的沸点.好奇的小叶准备测定某种食用油的沸点,已知食用油的沸点温度高于水的沸点温度(100℃),而小叶家只有刻度不超过100℃的温度计,她的方法是将该食用油倒入锅中均匀加热,每隔10 s测量一次油温,得到如下数据：(M8204006)

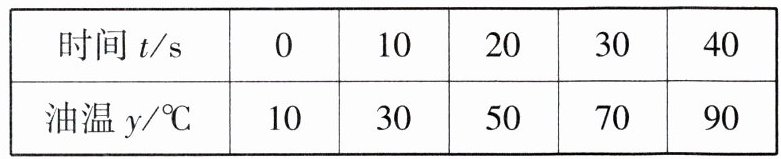
当加热100 s时,油沸腾了,由此可以估计该食用油的沸点温度是______℃.

答案： **答案**：$210$
**解析**：由题表中数据可知油温$y$随着时间$t$的增长而匀速增长，
设$y = kt + b(k\neq0)$，将$(0,10)$，$(10,30)$代入，得$\begin{cases}b = 10\\10k + b = 30\end{cases}$，解得$\begin{cases}k = 2\\b = 10\end{cases}$，$\therefore y = 2t + 10$，
经验证，点$(20,50)$，$(30,70)$，$(40,90)$也在直线$y = 2t + 10$上，当$t = 100$时，$y = 2\times100 + 10 = 210$，即该食用油的沸点温度是$210^{\circ}C$。

3.（新独家原创）“龟兔赛跑”的故事同学们都非常熟悉,如图所示的是乌龟和兔子赛跑时的路程(s)与时间(t)的对应关系,请你根据图中给出的信息预测,乌龟从出发到追上兔子用了______分钟.

答案： **答案**：$14$
**解析**：由图象可知，图中折线是兔子所跑的路程与时间的图象，图中直线是乌龟所爬的路程与时间的图象。兔子在起初每分钟跑$700\div1 = 700$(米)，乌龟每分钟爬$1500\div30 = 50$(米)，$\because700\div50 = 14$(分钟)，
$\therefore$乌龟从出发到追上兔子用了$14$分钟。

4.小明的爸爸用50万元购进一辆出租车(含经营权等其他费用).在投入营运后,每年营运的总收入为18.5万元,而各种费用的总支出为6万元,设该车营运x年后盈利y万元.
(1)写出y与x之间的函数关系式.
(2)请预测该出租车营运几年后开始盈利.

答案： **解析**：
(1)$y$与$x$之间的函数关系式为$y=(18.5 - 6)x-50 = 12.5x - 50$。
(2)当$y = 0$时，$12.5x - 50 = 0$，$\therefore x = 4$。
$\therefore$预测该出租车营运$4$年后开始盈利。

5.（2024湖南益阳沅江月考）为了解某品牌一款新能源汽车的耗电量,相关技术人员在汽车试验基地对该款新能源汽车做了耗电量试验,发现汽车剩余电量Q(kW·h)是汽车行驶路程s(km)的一次函数,试验数据记录如下.(M8204006)

(1)根据表中的数据,求Q与s之间的函数表达式.
(2)当汽车剩余电量为39.2 kW·h时,若以75 km/h的速度匀速行驶,预测该汽车最多还能行驶多长时间?

答案： **解析**：
(1)设$Q = ks + b(k\neq0)$，将$(0,80)$，$(100,63)$代入得$\begin{cases}b = 80\\100k + b = 63\end{cases}$，解得$\begin{cases}k=-0.17\\b = 80\end{cases}$。
经验证$(50,71.5)$，$(150,54.5)$，$(200,46)$也在直线$Q=-0.17s + 80$上，
$\therefore Q$与$s$之间的函数表达式为$Q=-0.17s + 80$。
(2)由题意得，$Q = 39.2\text{ kW}\cdot\text{h}$，$v = 75\text{ km/h}$，设该汽车还能行驶$t\text{ h}$，$\therefore s = 75t$，
$\therefore39.2=-0.17\times75t + 80$，$\therefore t = 3.2$。
答：该汽车最多还能行驶$3.2\text{ h}$。