《2025年5年中考3年模拟八年级数学下册湘教版》

1.(2024广西南宁良庆月考)关于矩形的判定,以下说法不正确的是 ( )
A.四个角都相等的四边形是矩形
B.一个内角是直角且对角线相等的四边形是矩形
C.对角线相等的平行四边形是矩形
D.对角线互相平分且相等的四边形是矩形

答案： B 一个内角是直角且对角线互相平分的四边形是矩形，故选项B的说法不正确。

2.(2024四川泸州中考)已知四边形ABCD是平行四边形,下列条件中,不能判定□ABCD为矩形的是 ( )
A.∠A = 90°
B.∠B = ∠C
C.AC = BD
D.AC⊥BD

答案： D \nA.
∵ 四边形ABCD是平行四边形，
∴ 当∠A = 90°时，□ABCD是矩形；\nB.
∵ 四边形ABCD是平行四边形，
∴ AB//CD，
∴ ∠B + ∠C = 180°，当∠B = ∠C时，有∠B = ∠C = 90°，此时□ABCD为矩形；\nC.
∵ 四边形ABCD是平行四边形，
∴ 当AC = BD时，□ABCD是矩形；\nD. 四边形ABCD是平行四边形，当AC⊥BD时，不能判定□ABCD为矩形，故选D。

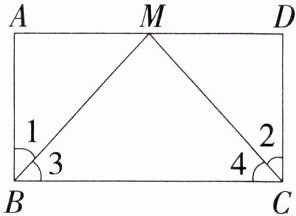
3.(2024贵州六盘水一模)如图,点M在□ABCD的边AD上,BM = CM,以下三个选项:①∠1 = ∠2;②AM = DM;③∠3 = ∠4,从其中选择一个合适的选项作为已知条件,使□ABCD为矩形.
(1)你添加的条件是________(填序号).
(2)添加条件后,请证明□ABCD为矩形.

答案： 解析 \n（1）①（或②）。\n（2）（答案不唯一）
证明：
∵ 四边形ABCD是平行四边形，
∴ AB//DC，AB = DC，
∴ ∠A + ∠D = 180°，
在△ABM和△DCM中，$\begin{cases}AB = DC\\\angle1=\angle2\\BM = CM\end{cases}$，
∴ △ABM≌DCM（SAS），
∴ ∠A = ∠D，
∵ ∠A + ∠D = 180°，
∴ ∠A = ∠D = 90°，
∴ □ABCD为矩形。

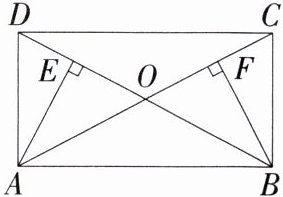
4.(2024湖南永州冷水滩模拟)如图,在平行四边形ABCD中,对角线BD,AC相交于点O,AE⊥BD,BF⊥AC,垂足分别为E,F.若CF = DE,求证:四边形ABCD为矩形.

答案： 证明
∵ 四边形ABCD是平行四边形，
∴ AD = BC，AD//BC，OA=$\frac{1}{2}$AC，OD=$\frac{1}{2}$BD，
∵ AE⊥BD，BF⊥AC，在Rt△ADE与Rt△BCF中，$\begin{cases}AD = BC\\DE = CF\end{cases}$，
∴ Rt△ADE≌Rt△BCF（HL），
∴ ∠ADE = ∠BCF = ∠DAO，
∴ DO = AO，
∴ AC = BD，
∴ 平行四边形ABCD是矩形。

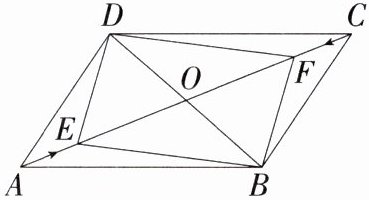
5.(2024湖南岳阳模拟)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向点C运动,点F同时以1个单位每秒的速度从点C出发沿CA向点A运动,若AC = 12,BD = 8,求出经过几秒后,四边形BEDF是矩形.

答案： 解析 设经过t秒后，四边形BEDF是矩形，则AE = CF = t，
∵ 四边形ABCD是平行四边形，
∴ OA = OC=$\frac{1}{2}$AC = 6，OB = OD=$\frac{1}{2}$BD = 4，
∴ OE = OF，
∴ 四边形BEDF是平行四边形，
当EF = BD，即OE = OD时，四边形BEDF是矩形，此时6 - t = 4或t - 6 = 4，
解得t = 2或t = 10，
即经过2秒或10秒后，四边形BEDF是矩形。

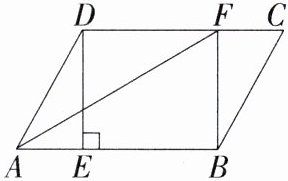
6.(2023广西贵港平南一模)如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD边上,DF = BE,连接AF,BF.(M8202005)
(1)求证:四边形BFDE是矩形.
(2)若AF平分∠DAB,CF = 3,DF = 5,求四边形BFDE的面积.

答案： 解析 \n（1）证明：
∵ 四边形ABCD是平行四边形，
∴ DF//EB，又
∵ DF = BE，
∴ 四边形BFDE是平行四边形，
∵ DE⊥AB，
∴ ∠DEB = 90°，
∴ 四边形BFDE是矩形。\n（2）
∵ AF平分∠DAB，DC//AB，
∴ ∠DAF = ∠FAB，∠DFA = ∠FAB，
∴ ∠DAF = ∠DFA，
∴ AD = DF = 5，
∵ AB = DC，DF = BE，
∴ AE = CF = 3，
∵ DE⊥AB，
∴ DE=$\sqrt{AD^{2}-AE^{2}}$= 4，
∴ 矩形BFDE的面积 = DF·DE = 5×4 = 20。

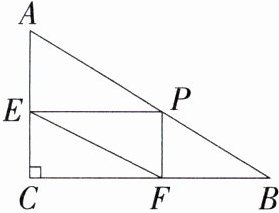
7.最短距离问题 (2024北京海淀期中,8,★★☆)如图,在Rt△ABC中,∠C = 90°,AC = 6,BC = 8,点P为AB边上任意一点,过点P作PE⊥AC于点E,PF⊥BC于点F,连接EF,则线段EF的最小值是 ( )

A.10
B.$\frac{12}{5}$
C.4.8
D.7.2

答案： C 连接CP（图略），
∵ PE⊥AC，PF⊥BC，∠ACB = 90°，
∴ ∠PEC = ∠ACB = ∠PFC = 90°，
∴ 四边形PECF是矩形，
∴ EF = CP. 当CP⊥AB时，CP的值最小，即EF的值最小，
∵ ∠C = 90°，AC = 6，BC = 8，
∴ AB=$\sqrt{AC^{2}+BC^{2}}$=$\sqrt{6^{2}+8^{2}}$= 10，
∴ $S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CP$，
∴ CP=$\frac{AC\cdot BC}{AB}=\frac{6×8}{10}$= 4.8，即EF的最小值是4.8，故选C。