《2025年5年中考3年模拟八年级数学下册湘教版》

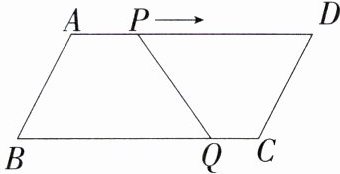
1.（2024 四川自贡中考）如图，在$\square ABCD$中，$\angle B = 60^{\circ},AB = 6\mathrm{cm},BC = 12\mathrm{cm}$. 点$P$从点$A$出发，以$1\mathrm{cm/s}$的速度沿$A\rightarrow D$运动，同时点$Q$从点$C$出发，以$3\mathrm{cm/s}$的速度沿$C\rightarrow B\rightarrow C\rightarrow\cdots$往复运动，当点$P$到达端点$D$时，点$Q$随之停止运动. 在此运动过程中，线段$PQ = CD$出现的次数是（ ）

A. 3
B. 4
C. 5
D. 6

答案：
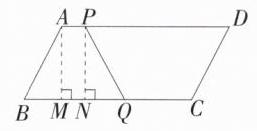
B 在$\square ABCD$中，$AB = 6\ cm$，$BC = 12\ cm$，$\therefore CD = AB = 6\ cm$，$AD = BC = 12\ cm$，$AD// BC$，$\because$点$P$从点$A$出发，以$1\ cm/s$的速度沿$A\rightarrow D$运动，$\therefore$点$P$从点$A$出发，到达点$D$的时间为$12\div1 = 12(s)$，$\because$点$Q$从点$C$出发，以$3\ cm/s$的速度沿$C\rightarrow B\rightarrow C\rightarrow\cdots$往复运动，$\therefore$点$Q$从点$C$出发，第一次到$B$点的时间为$12\div3 = 4(s)$，$\because AD// BC$，$\therefore DP// CQ$，当$DP = CQ$时，四边形$CDPQ$为平行四边形，$\therefore PQ = CD$，当$PQ = AB$且$PQ$与$AB$不平行时，四边形$CDPQ$为等腰梯形，$\therefore PQ = AB = CD$，设$P$，$Q$同时运动的时间为$t(s)$，当$0 ＜ t\leqslant4$时，$12 - t = 3t$，$\therefore t = 3$，此时$DP = CQ$，四边形$CDPQ$为平行四边形，$PQ = CD$，如图，过点$A$，$P$分别作$BC$的垂线，分别交$BC$于点$M$，$N$，$\therefore$四边形$AMNP$是矩形，$\therefore MN = AP = t$，$AM = PN$，$\because$四边形$ABQP$是等腰梯形，$\therefore PQ = AB$，$\angle PQN=\angle B$，$\because\angle BAM = 90^{\circ}-\angle B$，$\angle QPN = 90^{\circ}-\angle PQN$，$\therefore\angle BAM=\angle QPN$，在$\triangle ABM$和$\triangle PQN$中，$\begin{cases}AM = PN\\\angle BAM=\angle QPN\\AB = PQ\end{cases}$，$\therefore\triangle ABM\cong\triangle PQN(SAS)$，$\therefore BM = QN$，在$Rt\triangle ABM$中，$\angle B = 60^{\circ}$，$AB = 6\ cm$，$\therefore\angle BAM = 90^{\circ}-\angle B = 30^{\circ}$，$\therefore BM=\frac{1}{2}AB = 3\ cm$，$\therefore QN = BM = 3\ cm$，$\therefore t = 12 - 3t-3 - 3$，$\therefore t=\frac{3}{2}$，此时四边形$ABQP$是等腰梯形，$PQ = AB = CD$. 当$4 ＜ t\leqslant8$时，$12 - t = 12 - 3(t - 4)$，$\therefore t = 6$，此时$DP = CQ$，四边形$CDPQ$为平行四边形，$PQ = CD$. 当$8 ＜ t\leqslant12$时，$12 - t = 3(t - 8)$，$\therefore t = 9$，此时$DP = CQ$，四边形$CDPQ$为平行四边形，$PQ = CD$. 综上，当$t=\frac{3}{2}$或$t = 3$或$t = 6$或$t = 9$时，$PQ = CD$，共出现$4$次. 故选 B.

2. 如图，矩形$ABCD$中，点$P$是线段$AD$上一动点，$O$为$BD$的中点，连接$PO$并延长交$BC$于点$Q$，连接$BP,DQ$.
(1) 求证：$OP = OQ$.
(2) 若$AD = 8\mathrm{cm},AB = 6\mathrm{cm}$，点$P$从点$A$出发，以$1\mathrm{cm/s}$的速度向点$D$运动（不与点$D$重合）. 设点$P$的运动时间为$t\mathrm{s}$，请用含$t$的式子表示$PD$的长；并求$t$为何值时，$BD\perp PQ$.

答案： 解析\n（1）证明：$\because$四边形$ABCD$是矩形，$\therefore AD// BC$，$\therefore\angle PDO=\angle QBO$，$\because O$为$BD$的中点，$\therefore OB = OD$，在$\triangle POD$与$\triangle QOB$中，$\begin{cases}\angle PDO=\angle QBO\\OD = OB\\\angle POD=\angle QOB\end{cases}$，$\therefore\triangle POD\cong\triangle QOB(ASA)$，$\therefore OP = OQ$.\n（2）依题意得$AP = t\ cm$，$\therefore PD=(8 - t)cm$. $\because OB = OD$，$OP = OQ$，$\therefore$四边形$PBQD$是平行四边形，当四边形$PBQD$是菱形时，$BD\perp PQ$，$\therefore PD = BP=(8 - t)cm$，$\because$四边形$ABCD$是矩形，$\therefore\angle A = 90^{\circ}$，在$Rt\triangle ABP$中，由勾股定理得$AB^{2}+AP^{2}=BP^{2}$，即$6^{2}+t^{2}=(8 - t)^{2}$，$\therefore t=\frac{7}{4}$，$\therefore$当$t=\frac{7}{4}$时，$BD\perp PQ$.

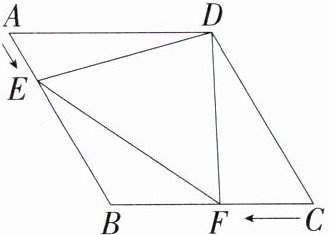
3. 如图，在菱形$ABCD$中，$AB = 5\mathrm{cm},\angle ADC = 120^{\circ}$，点$E、F$分别从点$A、C$同时出发，分别沿$AB、CB$方向向点$B$匀速移动（到达点$B$时停止），点$E$的速度为$1\mathrm{cm/s}$，点$F$的速度为$2\mathrm{cm/s}$，若经过$t\mathrm{s},\triangle DEF$为等边三角形，则$t$的值为（ ）

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{2}$
D. $\frac{5}{3}$

答案：
D 连接$DB$，如图所示，$\because$四边形$ABCD$为菱形，且$\angle ADC = 120^{\circ}$，$\therefore BC = CD$，$\angle CDB = 60^{\circ}$，$\therefore\triangle CDB$为等边三角形，$\therefore DB = DC$，$\because\triangle DEF$为等边三角形，$\therefore\angle EDF = 60^{\circ}$，$DE = DF$，$\therefore\angle CDB-\angle BDF=\angle EDF-\angle BDF$，$\therefore\angle CDF=\angle BDE$，在$\triangle EDB$和$\triangle FDC$中，$\begin{cases}DE = DF\\\angle EDB=\angle FDC\\DB = DC\end{cases}$，$\therefore\triangle EDB\cong\triangle FDC(SAS)$，$\therefore FC = BE$，由题意得$FC = 2t\ cm$，$AE = t\ cm$，$\therefore AB = AE + EB = AE + FC = t + 2t = 3t = 5\ cm$，$\therefore t=\frac{5}{3}$. 故选 D.

4. 如图，正方形$ABCD$中，点$O$是对角线$AC$的中点，点$P$是线段$AO$上（不与点$A、O$重合）的一个动点，过点$P$作$PE\perp PB$交边$CD$于点$E$.
(1) 求证：$PB = PE$.
(2) 过点$E$作$EF\perp AC$于点$F$，若正方形$ABCD$的边长为$2$，则在点$P$运动的过程中，$PF$的长度是否发生变化？若不变，请直接写出这个不变的值；若变化，请说明理由.

答案：
解析\n（1）证明：如图 1，过点$P$作$MN// AD$，交$AB$于点$M$，交$CD$于点$N$，$\because PB\perp PE$，$\therefore\angle BPE = 90^{\circ}$，$\therefore\angle MPB+\angle EPN = 90^{\circ}$，$\because$四边形$ABCD$是正方形，$\therefore\angle BAD=\angle ABC=\angle D = 90^{\circ}$，$\because AD// MN$，$\therefore\angle BMP=\angle BAD=\angle PNE=\angle D = 90^{\circ}$，$\therefore\angle MPB+\angle MBP = 90^{\circ}$，$\because\angle MPB+\angle EPN = 90^{\circ}$，$\therefore\angle EPN=\angle MBP$，$\because\angle PCN = 45^{\circ}$，$\therefore\triangle PNC$是等腰直角三角形，$\therefore PN = CN$，$\because\angle BMP=\angle PNC=\angle ABC = 90^{\circ}$，$\therefore$四边形$MBCN$是矩形，$\therefore BM = CN$，$\therefore BM = PN$，$\therefore\triangle BMP\cong\triangle PNE(ASA)$，$\therefore PB = PE$.\n（2）在点$P$运动的过程中，$PF$的长度不发生变化. 理由：如图 2，连接$OB$，$\because$点$O$是正方形$ABCD$的对角线$AC$的中点，$\therefore OB = OA$，$OB\perp AC$，$\therefore\angle AOB = 90^{\circ}$，$\therefore\angle OBP+\angle BPO = 90^{\circ}$，$\because\angle BPE = 90^{\circ}$，$\therefore\angle BPO+\angle OPE = 90^{\circ}$，$\therefore\angle OBP=\angle OPE$，$\because EF\perp AC$，$\therefore\angle EFP = 90^{\circ}=\angle AOB$，由（1）得$PB = PE$，$\therefore\triangle OBP\cong\triangle FPE(AAS)$，$\therefore PF = OB$，在$Rt\triangle AOB$中，$OB = OA$，$AB = 2$，$\therefore 2OB^{2}=4$，$\therefore OB=\sqrt{2}$，$\therefore PF=\sqrt{2}$，$\therefore PF$为定值.