第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
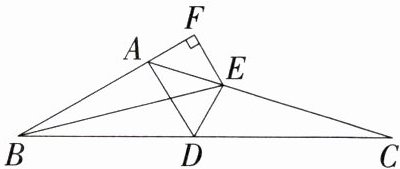
20.(2024广西河池凤山期末)(8分)如图,在△ABC中,点D在BC边上,∠BAD = 100°,∠ABC的平分线交AC于点E,过点E作EF⊥BA交BA的延长线于点F,且∠AEF = 50°,连接DE.
(1)求证:DE平分∠ADC.
(2)若AB = 7,AD = 4,CD = 8,且$S_{\triangle ACD}=15$,求△ABE的面积.
(1)求证:DE平分∠ADC.
(2)若AB = 7,AD = 4,CD = 8,且$S_{\triangle ACD}=15$,求△ABE的面积.

答案:
解析
(1)证明:过点E作EG⊥AD于点G,EH⊥BC于点H,如图,
∵EF⊥AB,∠AEF = 50°,
∴∠FAE = 90° - 50° = 40°,
∵∠BAD = 100°,
∴∠CAD = 180° - 100° - 40° = 40°,
∴∠FAE = ∠CAD,即AC为∠DAF的平分线,
又
∵EF⊥AB,EG⊥AD,
∴EF = EG,
∵BE是∠ABC的平分线,
∴EF = EH,
∴EG = EH,
∴点E在∠ADC的平分线上,
∴DE平分∠ADC.
(2)设EG = x,由
(1)得EF = EH = EG = x,
∵S△ACD = 15,AD = 4,CD = 8,
∴1/2AD·EG + 1/2CD·EH = 15,即2x + 4x = 15,
解得x = 2.5,
∴EF = x = 2.5,
∴S△ABE = 1/2AB·EF = 1/2×7×2.5 = 35/4.

解析
(1)证明:过点E作EG⊥AD于点G,EH⊥BC于点H,如图,
∵EF⊥AB,∠AEF = 50°,
∴∠FAE = 90° - 50° = 40°,
∵∠BAD = 100°,
∴∠CAD = 180° - 100° - 40° = 40°,
∴∠FAE = ∠CAD,即AC为∠DAF的平分线,
又
∵EF⊥AB,EG⊥AD,
∴EF = EG,
∵BE是∠ABC的平分线,
∴EF = EH,
∴EG = EH,
∴点E在∠ADC的平分线上,
∴DE平分∠ADC.
(2)设EG = x,由
(1)得EF = EH = EG = x,
∵S△ACD = 15,AD = 4,CD = 8,
∴1/2AD·EG + 1/2CD·EH = 15,即2x + 4x = 15,
解得x = 2.5,
∴EF = x = 2.5,
∴S△ABE = 1/2AB·EF = 1/2×7×2.5 = 35/4.

21.[新考向·教材拓展探究试题](2024山东潍坊昌乐期中)(10分)公元3世纪,古人就通过拼图验证了勾股定理:在直角三角形中,两直角边a,b与斜边c满足关系式$a^{2}+b^{2}=c^{2}$.还探索验证了勾股定理的逆定理:如果三角形的三边长满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形.
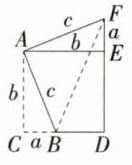
(1)小明发现了证明勾股定理的新方法:如图1,在正方形ACDE的边CD上取点B,连接AB,得到Rt△ACB,三边长分别为a,b,c,剪下△ACB把它拼接到△AEF的位置,如图2所示,请利用面积不变证明勾股定理.
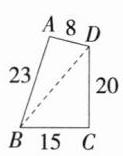
(2)一个零件的形状如图3所示,按规定这个零件中∠A和∠C都应是直角,小明测得这个零件各边的尺寸(单位:cm)如图3所示,请问这个零件符合要求吗? 并说明理由.

(1)小明发现了证明勾股定理的新方法:如图1,在正方形ACDE的边CD上取点B,连接AB,得到Rt△ACB,三边长分别为a,b,c,剪下△ACB把它拼接到△AEF的位置,如图2所示,请利用面积不变证明勾股定理.
(2)一个零件的形状如图3所示,按规定这个零件中∠A和∠C都应是直角,小明测得这个零件各边的尺寸(单位:cm)如图3所示,请问这个零件符合要求吗? 并说明理由.

答案:
解析
(1)证明:如图,连接BF,
∵AC = b,
∴正方形ACDE的面积为b²,
∵CD = DE = AC = b,EF = BC = a,
∴BD = CD - BC = b - a,DF = EF + DE = a + b,
∵∠CAE = 90°,
∴∠BAC + ∠BAE = 90°,
∵∠BAC = ∠EAF,
∴∠EAF + ∠BAE = 90°,即∠BAF = 90°,
∵AF = AB = c,
∴△BAF为等腰直角三角形,
∴四边形ABDF的面积为1/2c² + 1/2(b - a)(a + b) = 1/2c² + 1/2(b² - a²),
∵正方形ACDE的面积与四边形ABDF的面积相等,
∴b² = 1/2c² + 1/2(b² - a²),整理得a² + b² = c².
(2)这个零件不符合要求.
理由:连接BD,如图,
由勾股定理的逆定理知,只有当BC² + DC² = AB² + AD² = BD²时,∠A和∠C都是直角,
∵BC² + DC² = 15² + 20² = 225 + 400 = 625,
AB² + AD² = 23² + 8² = 529 + 64 = 593,且625 ≠ 593,
∴BC² + DC² ≠ AB² + AD²,
∴∠A和∠C不可能都是直角. 因此,这个零件不符合要求.
解析
(1)证明:如图,连接BF,
∵AC = b,
∴正方形ACDE的面积为b²,
∵CD = DE = AC = b,EF = BC = a,
∴BD = CD - BC = b - a,DF = EF + DE = a + b,
∵∠CAE = 90°,
∴∠BAC + ∠BAE = 90°,
∵∠BAC = ∠EAF,
∴∠EAF + ∠BAE = 90°,即∠BAF = 90°,
∵AF = AB = c,
∴△BAF为等腰直角三角形,
∴四边形ABDF的面积为1/2c² + 1/2(b - a)(a + b) = 1/2c² + 1/2(b² - a²),
∵正方形ACDE的面积与四边形ABDF的面积相等,
∴b² = 1/2c² + 1/2(b² - a²),整理得a² + b² = c².

(2)这个零件不符合要求.
理由:连接BD,如图,
由勾股定理的逆定理知,只有当BC² + DC² = AB² + AD² = BD²时,∠A和∠C都是直角,
∵BC² + DC² = 15² + 20² = 225 + 400 = 625,
AB² + AD² = 23² + 8² = 529 + 64 = 593,且625 ≠ 593,
∴BC² + DC² ≠ AB² + AD²,
∴∠A和∠C不可能都是直角. 因此,这个零件不符合要求.

22.(12分)已知在△ABC中,∠ABC = 90°,点E在直线AB上,ED与直线AC垂直,垂足为D,且M为EC的中点,连接BM,DM.
(1)如图1,若点E在线段AB上,探究线段BM与DM,∠BMD与∠BCD满足的数量关系,并直接写出你得到的结论.
(2)如图2,若点E在线段BA的延长线上,(1)中的结论是否仍然成立? 写出你的猜想并加以证明.

(1)如图1,若点E在线段AB上,探究线段BM与DM,∠BMD与∠BCD满足的数量关系,并直接写出你得到的结论.
(2)如图2,若点E在线段BA的延长线上,(1)中的结论是否仍然成立? 写出你的猜想并加以证明.

答案:
解析
(1)BM = DM,∠BMD = 2∠BCD.
详解:
∵M是EC的中点,∠ABC = ∠EDC = 90°,
∴BM = CM = DM = 1/2CE,
∴∠MCB = ∠MBC,∠MCD = ∠CDM,
∴∠BME = 2∠MCB,∠DME = 2∠MCD,
∴∠BME + ∠DME = 2(∠MCB + ∠MCD),
即∠BMD = 2∠BCD.
(2)
(1)中的结论仍然成立.
证明:
∵点M是Rt△BEC的斜边EC的中点,
∴BM = 1/2EC = MC,
∵点M是Rt△DEC的斜边EC的中点,
∴DM = 1/2EC = MC,
∴BM = DM.
∵BM = MC,DM = MC,
∴∠CBM ∠BCM,∠DCM ∠CDM,
∴∠BMD = ∠EMB - ∠EMD = 2∠BCM - 2∠DCM = 2(∠BCM - ∠DCM) = 2∠BCD,即∠BMD = 2∠BCD.
(1)BM = DM,∠BMD = 2∠BCD.
详解:
∵M是EC的中点,∠ABC = ∠EDC = 90°,
∴BM = CM = DM = 1/2CE,
∴∠MCB = ∠MBC,∠MCD = ∠CDM,
∴∠BME = 2∠MCB,∠DME = 2∠MCD,
∴∠BME + ∠DME = 2(∠MCB + ∠MCD),
即∠BMD = 2∠BCD.
(2)
(1)中的结论仍然成立.
证明:
∵点M是Rt△BEC的斜边EC的中点,
∴BM = 1/2EC = MC,
∵点M是Rt△DEC的斜边EC的中点,
∴DM = 1/2EC = MC,
∴BM = DM.
∵BM = MC,DM = MC,
∴∠CBM ∠BCM,∠DCM ∠CDM,
∴∠BMD = ∠EMB - ∠EMD = 2∠BCM - 2∠DCM = 2(∠BCM - ∠DCM) = 2∠BCD,即∠BMD = 2∠BCD.
查看更多完整答案,请扫码查看


