第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.如图,在正方形ABCD中,CE⊥MN,∠MCE=40°,则∠ANM= ( )
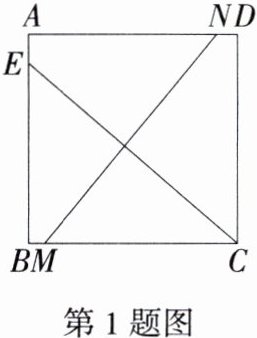

A.40° B.45° C.50° D.55°
答案:
**C**:设 $MN$ 与 $EC$ 交于点 $O$(图略),$\because CE\perp MN$,$\therefore\angle MOC = 90^{\circ}$,$\because\angle MCE = 40^{\circ}$,$\therefore\angle OMC = 50^{\circ}$,$\because$ 四边形 $ABCD$ 是正方形,$\therefore AD// BC$,$\therefore\angle ANM=\angle OMC = 50^{\circ}$。
2.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④$S_{△AOB}=S_{四边形DEOF}$,其中正确的结论有 ( )
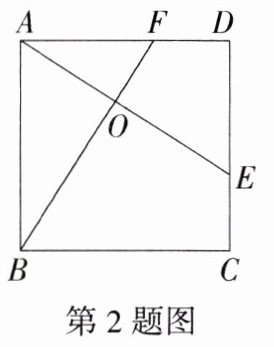
A.①②③
B.②③④
C.①③④
D.①②④

A.①②③
B.②③④
C.①③④
D.①②④
答案:
**D**:$\because$ 四边形 $ABCD$ 是正方形,$\therefore\angle BAF=\angle D = 90^{\circ}$,$AB = AD = CD$,$\because CE = DF$,$\therefore AD - DF = CD - CE$,即 $AF = DE$。在 $\triangle ABF$ 和 $\triangle DAE$ 中,$\begin{cases}AB = AD\\\angle BAF=\angle D\\AF = DE\end{cases}$,$\therefore\triangle ABF\cong\triangle DAE(SAS)$,$\therefore\angle ABF=\angle DAE$,$AE = BF$,故结论①正确;$\because\angle DAE+\angle BAO = 90^{\circ}$,$\therefore\angle ABF+\angle BAO = 90^{\circ}$,$\therefore\angle AOB = 180^{\circ}-(\angle ABF+\angle BAO)=180^{\circ}-90^{\circ}=90^{\circ}$,$\therefore AE\perp BF$,故结论②正确;假设 $AO = OE$,如图,连接 $BE$,$\because AE\perp BF$(已证),$\therefore AB = BE$,$\because$ 在 $Rt\triangle BCE$ 中,$BE>BC$,$\therefore AB>BC$,这与正方形的边长 $AB = BC$ 相矛盾,$\therefore$ 假设不成立,即 $AO\neq OE$,故结论③错误;$\because\triangle ABF\cong\triangle DAE$(已证),$\therefore S_{\triangle ABF}=S_{\triangle DAE}$,$\therefore S_{\triangle ABF}-S_{\triangle AOF}=S_{\triangle DAE}-S_{\triangle AOF}$,即 $S_{\triangle AOB}=S_{四边形DEOF}$,故结论④正确。综上所述,正确的结论有①②④。故选 D。
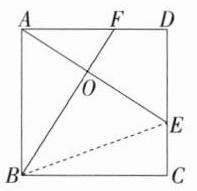
**D**:$\because$ 四边形 $ABCD$ 是正方形,$\therefore\angle BAF=\angle D = 90^{\circ}$,$AB = AD = CD$,$\because CE = DF$,$\therefore AD - DF = CD - CE$,即 $AF = DE$。在 $\triangle ABF$ 和 $\triangle DAE$ 中,$\begin{cases}AB = AD\\\angle BAF=\angle D\\AF = DE\end{cases}$,$\therefore\triangle ABF\cong\triangle DAE(SAS)$,$\therefore\angle ABF=\angle DAE$,$AE = BF$,故结论①正确;$\because\angle DAE+\angle BAO = 90^{\circ}$,$\therefore\angle ABF+\angle BAO = 90^{\circ}$,$\therefore\angle AOB = 180^{\circ}-(\angle ABF+\angle BAO)=180^{\circ}-90^{\circ}=90^{\circ}$,$\therefore AE\perp BF$,故结论②正确;假设 $AO = OE$,如图,连接 $BE$,$\because AE\perp BF$(已证),$\therefore AB = BE$,$\because$ 在 $Rt\triangle BCE$ 中,$BE>BC$,$\therefore AB>BC$,这与正方形的边长 $AB = BC$ 相矛盾,$\therefore$ 假设不成立,即 $AO\neq OE$,故结论③错误;$\because\triangle ABF\cong\triangle DAE$(已证),$\therefore S_{\triangle ABF}=S_{\triangle DAE}$,$\therefore S_{\triangle ABF}-S_{\triangle AOF}=S_{\triangle DAE}-S_{\triangle AOF}$,即 $S_{\triangle AOB}=S_{四边形DEOF}$,故结论④正确。综上所述,正确的结论有①②④。故选 D。

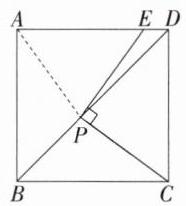
3.一题多解正方形ABCD的边长为6,点P在对角线BD上,点E是线段AD上或AD延长线上的一点,且PE⊥PC.
(1)如图1,点E在线段AD上,求证:PE=PC.
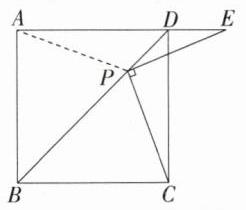
(2)如图2,点E在线段AD的延长线上,判断
(1)中的结论是否仍然成立,请说明理由.
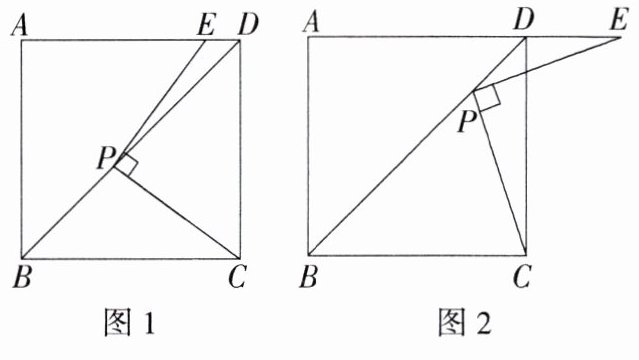
(1)如图1,点E在线段AD上,求证:PE=PC.
(2)如图2,点E在线段AD的延长线上,判断
(1)中的结论是否仍然成立,请说明理由.

答案:
**解析**\n**【解法一】**\n**
(1)证明**:如图,连接 $PA$,$\because$ 四边形 $ABCD$ 为正方形,$\therefore\angle ADP=\angle CDP = 45^{\circ}$,$DA = DC$,$\because PD = PD$,$\therefore\triangle DAP\cong\triangle DCP(SAS)$,$\therefore\angle DAP=\angle DCP$,$PC = PA$。在四边形 $CDEP$ 中,$\because\angle EPC+\angle ADC+\angle PED+\angle PCD = 360^{\circ}$,$\angle ADC=\angle EPC = 90^{\circ}$,$\therefore\angle PCD+\angle DEP = 180^{\circ}$,$\because\angle AEP+\angle DEP = 180^{\circ}$,$\therefore\angle AEP=\angle DCP$,$\therefore\angle AEP=\angle PAE$,$\therefore PE = PA$,$\therefore PE = PC$。
\n**
(2)
(1)中的结论成立**:理由如下:如图,连接 $AP$,由
(1)可知 $\triangle ADP\cong\triangle CDP$,$\therefore\angle DAP=\angle DCP$,$AP = PC$。$\because\angle DCP+\angle DPC+\angle PDC = 180^{\circ}$,$\angle CPE = 90^{\circ}$,$\angle CDP = 45^{\circ}$,$\therefore\angle DPE+\angle DCP = 45^{\circ}$,$\because\angle ADP=\angle DPE+\angle AEP = 45^{\circ}$,$\therefore\angle DCP=\angle AEP$,$\therefore\angle PAD=\angle AEP$,$\therefore AP = PE$,$\therefore PE = PC$。
\n**【解法二】**\n**
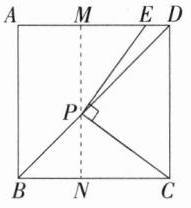
(1)证明**:如图,过点 $P$ 作 $PN\perp BC$,垂足为点 $N$,延长 $NP$ 交 $AD$ 于 $M$,则 $\angle PMD=\angle PNC = 90^{\circ}$。$\because$ 四边形 $ABCD$ 为正方形,$\therefore\angle ADB = 45^{\circ}$,$\therefore\angle MPD = 45^{\circ}$,$\therefore\angle ADB=\angle MPD$,$\therefore MD = MP$。易证四边形 $MNCD$ 是矩形,$\therefore MD = NC$,$\therefore MP = NC$。$\because PE\perp PC$,$\therefore\angle MPE+\angle NPC = 90^{\circ}$,$\because\angle MPE+\angle MEP = 90^{\circ}$,$\therefore\angle MEP=\angle NPC$,$\therefore\triangle MPE\cong\triangle NCP(AAS)$,$\therefore PE = PC$。
\n**
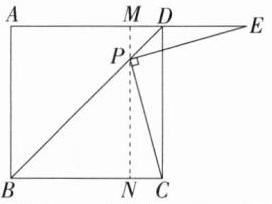
(2)
(1)中结论成立**:理由如下:如图,过点 $P$ 作 $PN\perp BC$,垂足为点 $N$,延长 $NP$ 交 $AD$ 于 $M$,同
(1)可证 $\triangle MPE\cong\triangle NCP$,$\therefore PE = PC$。
**解析**\n**【解法一】**\n**
(1)证明**:如图,连接 $PA$,$\because$ 四边形 $ABCD$ 为正方形,$\therefore\angle ADP=\angle CDP = 45^{\circ}$,$DA = DC$,$\because PD = PD$,$\therefore\triangle DAP\cong\triangle DCP(SAS)$,$\therefore\angle DAP=\angle DCP$,$PC = PA$。在四边形 $CDEP$ 中,$\because\angle EPC+\angle ADC+\angle PED+\angle PCD = 360^{\circ}$,$\angle ADC=\angle EPC = 90^{\circ}$,$\therefore\angle PCD+\angle DEP = 180^{\circ}$,$\because\angle AEP+\angle DEP = 180^{\circ}$,$\therefore\angle AEP=\angle DCP$,$\therefore\angle AEP=\angle PAE$,$\therefore PE = PA$,$\therefore PE = PC$。

\n**
(2)
(1)中的结论成立**:理由如下:如图,连接 $AP$,由
(1)可知 $\triangle ADP\cong\triangle CDP$,$\therefore\angle DAP=\angle DCP$,$AP = PC$。$\because\angle DCP+\angle DPC+\angle PDC = 180^{\circ}$,$\angle CPE = 90^{\circ}$,$\angle CDP = 45^{\circ}$,$\therefore\angle DPE+\angle DCP = 45^{\circ}$,$\because\angle ADP=\angle DPE+\angle AEP = 45^{\circ}$,$\therefore\angle DCP=\angle AEP$,$\therefore\angle PAD=\angle AEP$,$\therefore AP = PE$,$\therefore PE = PC$。

\n**【解法二】**\n**
(1)证明**:如图,过点 $P$ 作 $PN\perp BC$,垂足为点 $N$,延长 $NP$ 交 $AD$ 于 $M$,则 $\angle PMD=\angle PNC = 90^{\circ}$。$\because$ 四边形 $ABCD$ 为正方形,$\therefore\angle ADB = 45^{\circ}$,$\therefore\angle MPD = 45^{\circ}$,$\therefore\angle ADB=\angle MPD$,$\therefore MD = MP$。易证四边形 $MNCD$ 是矩形,$\therefore MD = NC$,$\therefore MP = NC$。$\because PE\perp PC$,$\therefore\angle MPE+\angle NPC = 90^{\circ}$,$\because\angle MPE+\angle MEP = 90^{\circ}$,$\therefore\angle MEP=\angle NPC$,$\therefore\triangle MPE\cong\triangle NCP(AAS)$,$\therefore PE = PC$。

\n**
(2)
(1)中结论成立**:理由如下:如图,过点 $P$ 作 $PN\perp BC$,垂足为点 $N$,延长 $NP$ 交 $AD$ 于 $M$,同
(1)可证 $\triangle MPE\cong\triangle NCP$,$\therefore PE = PC$。

4.探究:
如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,连接NC、BE 交于点P.求证:∠ANC=∠ABE.
应用:
(1)Q是线段BC的中点,连接PQ,若BC=6,求PQ的长.
(2)若AB=5$\sqrt{2}$,BC=6,∠ABC=45°,求BE的长;
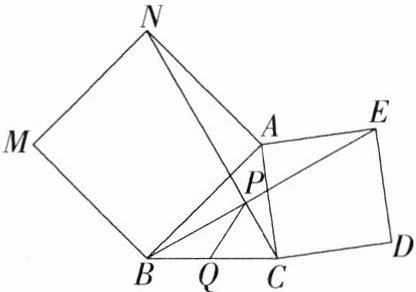
如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,连接NC、BE 交于点P.求证:∠ANC=∠ABE.
应用:
(1)Q是线段BC的中点,连接PQ,若BC=6,求PQ的长.
(2)若AB=5$\sqrt{2}$,BC=6,∠ABC=45°,求BE的长;

答案:
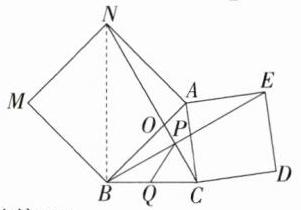
**解析**\n**探究**:证明:$\because$ 四边形 $ANMB$ 和四边形 $ACDE$ 是正方形,$\therefore AN = AB$,$AC = AE$,$\angle NAB=\angle CAE = 90^{\circ}$,$\therefore\angle NAB+\angle BAC=\angle BAC+\angle CAE$,$\therefore\angle NAC=\angle BAE$。
在 $\triangle ANC$ 和 $\triangle ABE$ 中,$\begin{cases}AN = AB\\\angle NAC=\angle BAE\\AC = AE\end{cases}$,$\therefore\triangle ANC\cong\triangle ABE(SAS)$,$\therefore\angle ANC=\angle ABE$。\n**应用**:\n**
(1)**:设 $AB$ 与 $NC$ 的交点为 $O$,如图,$\because$ 四边形 $NABM$ 是正方形,$\therefore\angle NAB = 90^{\circ}$,$\therefore\angle ANC+\angle AON = 90^{\circ}$,$\because\angle BOP=\angle AON$,$\angle ANC=\angle ABE$,$\therefore\angle ABP+\angle BOP = 90^{\circ}$,$\therefore\angle BPC = 90^{\circ}$,$\because Q$ 为 $BC$ 的中点,$BC = 6$,$\therefore PQ=\frac{1}{2}BC = 3$。\n**
(2)**:如图,连接 $BN$,$\because$ 四边形 $ABMN$ 是正方形,$AB = 5\sqrt{2}$,$\therefore BN = 10$,$\angle ABN = 45^{\circ}$,又 $\because\angle ABC = 45^{\circ}$,$\therefore\angle NBC = 90^{\circ}$,即 $BN\perp BC$,$\therefore CN=\sqrt{BC^{2}+BN^{2}}=2\sqrt{34}$,$\because\triangle ANC\cong\triangle ABE$,$\therefore BE = CN = 2\sqrt{34}$。
**解析**\n**探究**:证明:$\because$ 四边形 $ANMB$ 和四边形 $ACDE$ 是正方形,$\therefore AN = AB$,$AC = AE$,$\angle NAB=\angle CAE = 90^{\circ}$,$\therefore\angle NAB+\angle BAC=\angle BAC+\angle CAE$,$\therefore\angle NAC=\angle BAE$。
在 $\triangle ANC$ 和 $\triangle ABE$ 中,$\begin{cases}AN = AB\\\angle NAC=\angle BAE\\AC = AE\end{cases}$,$\therefore\triangle ANC\cong\triangle ABE(SAS)$,$\therefore\angle ANC=\angle ABE$。\n**应用**:\n**
(1)**:设 $AB$ 与 $NC$ 的交点为 $O$,如图,$\because$ 四边形 $NABM$ 是正方形,$\therefore\angle NAB = 90^{\circ}$,$\therefore\angle ANC+\angle AON = 90^{\circ}$,$\because\angle BOP=\angle AON$,$\angle ANC=\angle ABE$,$\therefore\angle ABP+\angle BOP = 90^{\circ}$,$\therefore\angle BPC = 90^{\circ}$,$\because Q$ 为 $BC$ 的中点,$BC = 6$,$\therefore PQ=\frac{1}{2}BC = 3$。\n**
(2)**:如图,连接 $BN$,$\because$ 四边形 $ABMN$ 是正方形,$AB = 5\sqrt{2}$,$\therefore BN = 10$,$\angle ABN = 45^{\circ}$,又 $\because\angle ABC = 45^{\circ}$,$\therefore\angle NBC = 90^{\circ}$,即 $BN\perp BC$,$\therefore CN=\sqrt{BC^{2}+BN^{2}}=2\sqrt{34}$,$\because\triangle ANC\cong\triangle ABE$,$\therefore BE = CN = 2\sqrt{34}$。

5.如图,在正方形ABCD中,点E、F分别在边BC、
CD上,且∠EAF=45°,连接EF、BD、AE、AF,BD 与AF、AE分别相交于点M、N.
(1)求证:EF=BE+DF.
(2)若正方形ABCD的边长为6,BE=2,,求DF 的长.
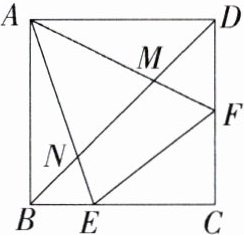
CD上,且∠EAF=45°,连接EF、BD、AE、AF,BD 与AF、AE分别相交于点M、N.
(1)求证:EF=BE+DF.
(2)若正方形ABCD的边长为6,BE=2,,求DF 的长.

答案:
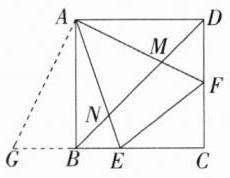
**解析**\n**
(1)证明**:如图,延长 $CB$ 至点 $G$,使 $BG = DF$,连接 $AG$。$\because$ 四边形 $ABCD$ 为正方形,$\therefore AB = AD$,$\angle BAD=\angle ADF=\angle ABE=\angle ABG = 90^{\circ}$。
在 $\triangle ABG$ 和 $\triangle ADF$ 中,$\begin{cases}AB = AD\\\angle ABG=\angle ADF\\BG = DF\end{cases}$,$\therefore\triangle ABG\cong\triangle ADF(SAS)$,$\therefore\angle DAF=\angle BAG$,$AF = AG$,$\because\angle EAF = 45^{\circ}$,$\therefore\angle GAE=\angle BAG+\angle BAE=\angle DAF+\angle BAE = 90^{\circ}-\angle EAF = 45^{\circ}$,即 $\angle GAE=\angle EAF$。
在 $\triangle AEF$ 和 $\triangle AEG$ 中,$\begin{cases}AF = AG\\\angle FAE=\angle GAE\\AE = AE\end{cases}$,$\therefore\triangle AEF\cong\triangle AEG(SAS)$,$\therefore EF = EG$,$\because EG = BE + BG$,$\therefore EF = BE + BG = BE + DF$。\n**
(2)**:$\because BC = 6$,$BE = 2$,$\therefore EC = 4$,由
(1)得 $EF = BE + DF = 2+DF$,在 $Rt\triangle CEF$ 中,$EF^{2}=CE^{2}+CF^{2}$,$\therefore(2 + DF)^{2}=4^{2}+(6 - DF)^{2}$,$\therefore DF = 3$。
**解析**\n**
(1)证明**:如图,延长 $CB$ 至点 $G$,使 $BG = DF$,连接 $AG$。$\because$ 四边形 $ABCD$ 为正方形,$\therefore AB = AD$,$\angle BAD=\angle ADF=\angle ABE=\angle ABG = 90^{\circ}$。
在 $\triangle ABG$ 和 $\triangle ADF$ 中,$\begin{cases}AB = AD\\\angle ABG=\angle ADF\\BG = DF\end{cases}$,$\therefore\triangle ABG\cong\triangle ADF(SAS)$,$\therefore\angle DAF=\angle BAG$,$AF = AG$,$\because\angle EAF = 45^{\circ}$,$\therefore\angle GAE=\angle BAG+\angle BAE=\angle DAF+\angle BAE = 90^{\circ}-\angle EAF = 45^{\circ}$,即 $\angle GAE=\angle EAF$。
在 $\triangle AEF$ 和 $\triangle AEG$ 中,$\begin{cases}AF = AG\\\angle FAE=\angle GAE\\AE = AE\end{cases}$,$\therefore\triangle AEF\cong\triangle AEG(SAS)$,$\therefore EF = EG$,$\because EG = BE + BG$,$\therefore EF = BE + BG = BE + DF$。\n**
(2)**:$\because BC = 6$,$BE = 2$,$\therefore EC = 4$,由
(1)得 $EF = BE + DF = 2+DF$,在 $Rt\triangle CEF$ 中,$EF^{2}=CE^{2}+CF^{2}$,$\therefore(2 + DF)^{2}=4^{2}+(6 - DF)^{2}$,$\therefore DF = 3$。

查看更多完整答案,请扫码查看


