《2025年5年中考3年模拟八年级数学下册湘教版》

1.已知四边形ABCD是平行四边形，再从①AB = BC；②∠ABC = 90°；③AC = BD；④AC⊥BD这四个条件中，选两个作为补充条件，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是 （ ）
A.选①②
B.选②③
C.选①③
D.选②④

答案： B
A.
∵ 四边形 $ABCD$ 是平行四边形，$AB = BC$，
∴ 平行四边形 $ABCD$ 是菱形.
∵ $\angle ABC = 90^{\circ}$，
∴ 菱形 $ABCD$ 是正方形，故选项 A 不符合题意；
B. 当 $\angle ABC = 90^{\circ}$，$AC = BD$ 时，只能得到平行四边形 $ABCD$ 是矩形，故选项 B 符合题意；
C. 当 $AB = BC$，$AC = BD$ 时，可以证明平行四边形 $ABCD$ 是正方形，故选项 C 不符合题意；
D. 当 $\angle ABC = 90^{\circ}$，$AC\perp BD$ 时，可以证明平行四边形 $ABCD$ 是正方形，故选项 D 不符合题意. 故选 B.

2.(2021广西玉林中考)如图，一个四边形顺次添加下列条件中的三个条件便得到正方形：
a.两组对边分别相等；b.一组对边平行且相等；
c.一组邻边相等；d.一个角是直角.顺次添加的条件：①a→c→d；②b→d→c；③a→b→c.则正确的是 （ ）

A.仅①
B.仅③
C.①②
D.②③

答案： C
① 由 a 得到两组对边分别相等的四边形是平行四边形，然后添加 c 得到一组邻边相等的平行四边形是菱形，再添加 d 得到有一个角是直角的菱形是正方形，故①正确；
② 由 b 得到一组对边平行且相等的四边形是平行四边形，然后添加 d 得到有一个角是直角的平行四边形是矩形，再添加 c 得到一组邻边相等的矩形是正方形，故②正确；
③ 由 a 得到两组对边分别相等的四边形是平行四边形，然后添加 b 得到一组对边平行且相等的平行四边形仍是平行四边形，再添加 c 得到一组邻边相等的平行四边形是菱形，不能得到该四边形是正方形，故③不正确. 故选 C.

3.(2023黑龙江龙东地区中考)如图，在矩形ABCD中，对角线AC，BD相交于点O，试添加一个条件：________，使得矩形ABCD为正方形.(写出一个条件即可)(M8202005)

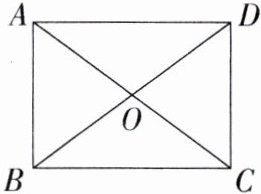
答案： 答案 $AB = AD$（答案不唯一）
解析 （答案不唯一）添加 $AB = AD$. 理由：
∵ 四边形 $ABCD$ 是矩形，$AB = AD$，
∴ 四边形 $ABCD$ 是正方形.

4.如图，△ABC中，∠ACB = 90°，CD平分∠ACB，DE⊥BC，DF⊥AC，求证：四边形CFDE为正方形.

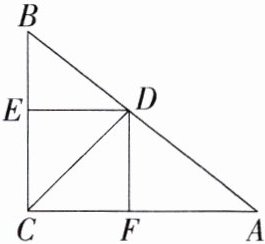
答案： 证明
∵ $\angle ACB = 90^{\circ}$，$DE\perp BC$，$DF\perp AC$，
∴ 四边形 $CFDE$ 是矩形.
∵ $CD$ 平分 $\angle ACB$，
∴ $DE = DF$.
∴ 四边形 $CFDE$ 是正方形.

5.(2024河南南阳期末,7,★☆☆)四边形ABCD的对角线AC和BD相交于点O，假设有下列条件：①AB = AD；②∠DAB = 90°；③AO = CO，BO = DO；④四边形ABCD为矩形；⑤四边形ABCD为菱形；⑥四边形ABCD为正方形，则下列推理不成立的是(M8202005) （ ）
A.由①④得⑥
B.由①③得⑤
C.由①②得⑥
D.由②③得④

答案： C
A.
∵ 四边形 $ABCD$ 为矩形，$AB = AD$，
∴ 四边形 $ABCD$ 为正方形，不符合题意；
B.
∵ $AO = CO$，$BO = DO$，
∴ 四边形 $ABCD$ 是平行四边形，
∵ $AB = AD$，
∴ 四边形 $ABCD$ 是菱形，不符合题意；
C. 由 $AB = AD$，$\angle DAB = 90^{\circ}$，无法证明四边形 $ABCD$ 是正方形，符合题意；
D.
∵ $AO = CO$，$BO = DO$，
∴ 四边形 $ABCD$ 是平行四边形，
∵ $\angle DAB = 90^{\circ}$，
∴ 四边形 $ABCD$ 为矩形，不符合题意. 故选 C.

6.(2023湖北十堰中考,20,★★☆)如图，□ABCD的对角线AC，BD交于点O，分别以点B，C为圆心，$\frac{1}{2}AC$，$\frac{1}{2}BD$长为半径画弧，两弧交于点P，连接BP，CP.(M8202005)
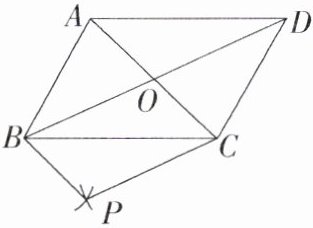
(1)试判断四边形BPCO的形状，并说明理由.
(2)请说明当□ABCD的对角线满足什么条件时，四边形BPCO是正方形？请说明理由.

答案： 解析
（1）四边形 $BPCO$ 为平行四边形.
理由：
∵ 四边形 $ABCD$ 为平行四边形，
∴ $OC = OA=\frac{1}{2}AC$，$OB = OD=\frac{1}{2}BD$，
∵ 以点 $B$，$C$ 为圆心，$\frac{1}{2}AC$，$\frac{1}{2}BD$ 长为半径画弧，两弧交于点 $P$，
∴ $OB = CP$，$BP = OC$，
∴ 四边形 $BPCO$ 为平行四边形.
（2）当 $AC\perp BD$，$AC = BD$ 时，四边形 $BPCO$ 为正方形.
理由：
∵ $AC\perp BD$，
∴ $\angle BOC = 90^{\circ}$，
∵ $AC = BD$，$OB=\frac{1}{2}BD$，$OC=\frac{1}{2}AC$，
∴ $OB = OC$，
∴ 平行四边形 $BPCO$ 为正方形.

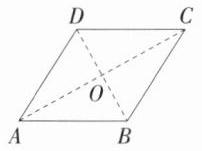
7.(2024江苏连云港期中,23,★★☆)我们知道，菱形和正方形虽然都是四边相等的四边形，但形状有差异，可以将菱形和正方形的接近程度称为菱形的“神似度”.如图，菱形ABCD中，对角线AC，BD的长分别为a，b(a≥b)，我们把$\frac{a}{b}$定义为菱形的“神似度”.
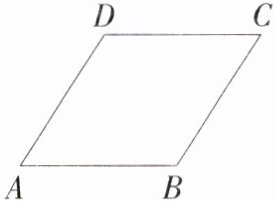
(1)当菱形的“神似度” = ________时，菱形ABCD就是正方形.
(2)当∠BAD = 60°时，求菱形ABCD的“神似度”.

答案：
解析
（1）由题意可得，当 $AC = BD$ 时，菱形 $ABCD$ 为正方形，
∴ $\frac{a}{b}=1$. 故答案为 1.
（2）如图，连接 $AC$，$BD$，交于点 $O$，设 $AB = x$，
在菱形 $ABCD$ 中，$AB = AD$，
∵ $\angle BAD = 60^{\circ}$，
∴ $\triangle ABD$ 是等边三角形，
∴ $BD = x$，$BO = DO=\frac{1}{2}x$，
∴ $AO=\sqrt{AD^{2}-DO^{2}}=\frac{\sqrt{3}}{2}x$，
∴ $AC=\sqrt{3}x$，
∴ $\frac{a}{b}=\frac{AC}{BD}=\frac{\sqrt{3}x}{x}=\sqrt{3}$，
即菱形 $ABCD$ 的“神似度”为 $\sqrt{3}$.