《2025年5年中考3年模拟八年级数学下册湘教版》

1.(2024湖南长沙雅礼教育集团期末)如图,在直角三角形ACB中,∠C = 90°,∠A = 30°,BC = 2,则AB等于(M8201001) ( )

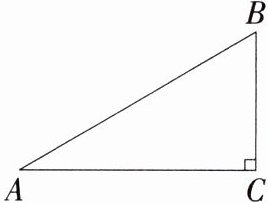
A.2
B.3
C.4
D.2$\sqrt{5}$

答案： C

∵在Rt△ABC中，∠A = 30°，BC = 2，
∴AB = 2BC = 4，故选C.

2.(2024湖南湘西州花垣期中)如图,一棵树在一次强台风中在离地面3米处折断倒下,倒下部分与地面成30°角,则这棵树在折断前的高度为( )

A.6米
B.9米
C.12米
D.15米

答案：
B 如图，根据题意得BC = 3米，
∵∠ACB = 90°，∠BAC = 30°，
∴AB = 2BC = 2×3 = 6（米），
∴这棵树在折断前的高度为3 + 6 = 9（米）.故选B.

3.在△ABC中,∠A：∠B：∠C = 1：2：3,若最短边BC = 5 cm,则最长边AB的长是 ( )
A.7 cm
B.8 cm
C.9 cm
D.10 cm

答案： D 设∠A = α，则∠B = 2α，∠C = 3α，
∴α + 2α + 3α = 180°，解得α = 30°，
∴三角形的三个角分别为30°、60°、90°，在直角三角形中，
∵30°角所对的最短边BC = 5 cm，
∴最长边AB = 2BC = 2×5 = 10 cm.故选D.

4.如图,某衣架内部可以近似看成一个等腰三角形,记为等腰三角形ABC,若它的顶角∠BAC = 120°,腰长AB = 26 cm,则底边上的高AD的长为________.

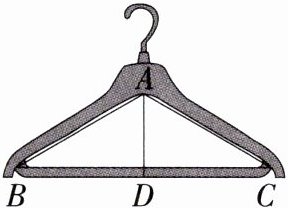
答案： 答案 13 cm
解析 由题意知，在△ABC中，∠BAC = 120°，AB = AC，
∴∠B = ∠C = $\frac{1}{2}(180° - ∠BAC)=30°$，
又
∵AD⊥BC，
∴AD = $\frac{1}{2}AB=\frac{1}{2}×26 = 13$(cm).

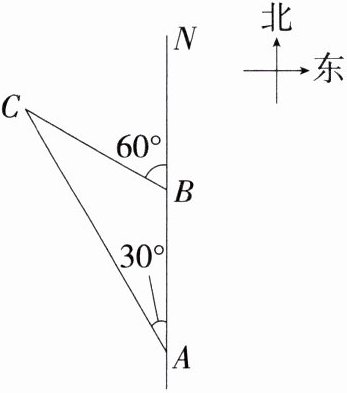
5.如图,一艘船上午8时从海岛A出发,以20海里/时的速度沿正北方向航行,上午10时到达海岛B处,已知分别从海岛A,B处远望灯塔C,测得∠NAC = 30°,∠NBC = 60°.
(1)求海岛B到灯塔C的距离.
(2)若这艘船继续沿正北方向航行,问上午几时该船与灯塔C的距离最短?

答案：
解析 （1）由题意得AB = 20×2 = 40海里.
∵∠NBC = 60°，∠NAC = 30°，
∴∠ACB = ∠NBC - ∠NAC = 30°，
∴∠ACB = ∠NAC，
∴BC = AB = 40（海里）.
答：海岛B到灯塔C的距离为40海里.
（2）如图，过点C作CP⊥AN于点P，
则∠BPC = 90°，此时线段CP的长为该船与灯塔C的最短距离，
∵∠NBC = 60°，
∴在Rt△CBP中，∠PCB = 180° - ∠BPC - ∠CBP = 30°，
∴PB = $\frac{1}{2}BC = 20$海里，
∴该船从海岛B处航行至P处的时间为20÷20 = 1（小时），
∵10 + 1 = 11.
答：若这艘船继续沿正北方向航行，上午11时该船与灯塔C的距离最短.

6.(2024山东青岛胶州月考,6,★☆☆)如图,已知∠AOB = 60°,点P在射线OA上,OP = 10,点M、N在射线OB上,PM = PN,若MN = 3,则OM的长为(M8201001) ( )

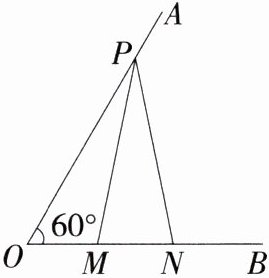
A.2
B.3.5
C.6
D.8

答案：
B 如图，过点P作PH⊥MN于点H.
∵PM = PN，MN = 3，
∴MH = NH = $\frac{1}{2}MN = 1.5$，
∵在Rt△POH中，∠POH = 60°，
∴∠OPH = 90° - 60° = 30°，
∴OH = $\frac{1}{2}OP=\frac{1}{2}×10 = 5$，
∴OM = OH - MH = 5 - 1.5 = 3.5.故选B.

7.(2022黑龙江哈尔滨月考,10,★★☆)如图,Rt△ABC中,∠C = 90°,以点B为圆心,适当长为半径画弧,与∠ABC的两边相交于点E,F,分别以点E和点F为圆心,大于$\frac{1}{2}EF$的长为半径画弧,两弧相交于点M,作射线BM交AC于点D.若△BDC的面积为10,∠ABC = 2∠A,则△ABC的面积为 ( )

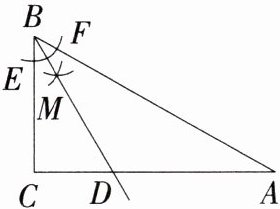
A.25
B.30
C.35
D.40

答案： B 由作图可知，BD为∠ABC的平分线，
∴∠CBD = ∠ABD = $\frac{1}{2}∠ABC$，又
∵在Rt△ABC中，∠ABC + ∠A = 90°，∠ABC = 2∠A，
∴∠A = ∠CBD = ∠ABD = 30°，
∴AD = BD = 2CD，
∴AC = 3CD，
∵△BDC的面积 = $\frac{1}{2}CD·BC = 10$，
∴△ABC的面积 = $\frac{1}{2}AC·BC=\frac{1}{2}×3CD·BC = 30$，故选B.