《2025年5年中考3年模拟八年级数学下册湘教版》

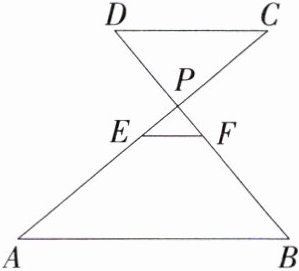
8.构造中位线法（2022湖南师大附中梅溪湖中学月考，10，★★☆）如图，AB//CD，AC、BD相交于点P，E、F分别为AC、BD的中点，若AB = 10，CD = 6，则EF的长是（M8202004）（ ）

A.1
B.2
C.3
D.4

答案： B

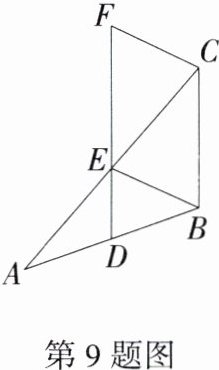
9.（2020湖南株洲中考，16，★★☆）如图所示，D、E分别是△ABC的边AB、AC的中点，连接BE，过点C作CF//BE，交DE的延长线于点F，若EF = 3，则DE的长为________.

答案： 答案 $\frac{3}{2}$
解析
∵D、E分别是△ABC的边AB、AC的中点,
∴DE为△ABC的中位线,
∴DE//BC,DE = $\frac{1}{2}$BC,
又
∵CF//BE,
∴四边形BCFE为平行四边形,
∴BC = EF = 3,
∴DE = $\frac{1}{2}$BC = $\frac{3}{2}$.

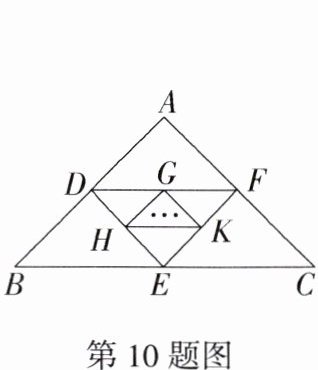
10.新考向·代数推理（2023湖南益阳赫山期中，18，★★☆）如图，顺次连接腰长为2的等腰直角三角形ABC各边的中点得到第1个小三角形DEF，再顺次连接所得的小三角形DEF各边的中点得到第2个小三角形GHK，如此操作下去，则第n个小三角形的面积为________.

答案： 答案 $\frac{1}{2^{2n - 1}}$
解析 记三角形ABC的面积为S,第一个小三角形DEF的面积为S₁,第二个小三角形GHK的面积为S₂,……,
∵S₁ = $\frac{1}{4}$S = $\frac{1}{2^{2}}$S,S₂ = $\frac{1}{4}$×$\frac{1}{4}$S = $\frac{1}{2^{4}}$S,S₃ = $\frac{1}{2^{6}}$S,……,
∴Sₙ = $\frac{1}{2^{2n}}$S = $\frac{1}{2^{2n}}$×$\frac{1}{2}$×2×2 = $\frac{1}{2^{2n - 1}}$.

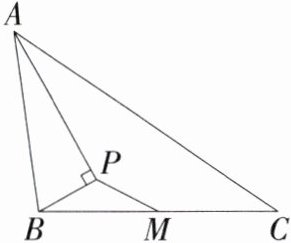
11.（2024广西南宁三中月考，18，★★☆）如图，在△ABC中，M是BC边的中点，AP是∠BAC的平分线，BP⊥AP于点P，连接PM.已知AB = 16，AC = 24，则PM的长为________.

答案： 答案 4
解析 延长BP交AC于点N(图略),
∵AP是∠BAC的平分线,BP⊥AP,
∴∠BAP = ∠NAP,∠APB = ∠APN = 90°,
∵AP = AP,
∴△ABP≌△ANP(ASA),
∴AN = AB = 16,BP = PN,
∴CN = AC - AN = 24 - 16 = 8,
∵BP = PN,BM = CM,
∴PM是△BNC的中位线,
∴PM = $\frac{1}{2}$CN = 4.

12.（2024湖南长沙期中，22，★★☆）如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，连接CD，过点E作EF//CD交BC的延长线于点F.
（1）求证：DE = CF.
（2）求EF的长.

答案： 解析
(1)证明:
∵D、E分别为AB、AC的中点,
∴DE//BC,
∵EF//CD,
∴四边形DEFC是平行四边形,
∴DE = CF.
(2)
∵四边形DEFC是平行四边形,
∴EF = DC,
∵D为AB的中点,等边△ABC的边长是2,
∴AD = BD = 1,CD⊥AB,BC = 2,
∴EF = DC = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$.

13.（2023湖南常德鼎城期末，24，★★☆）如图，在△ABC中，AD⊥BC，垂足为D，E，F分别为边AC，BC的中点，连接DE，EF.
（1）若∠B = 40°，∠C = 55°，求∠DEF的度数.
（2）若AD = 6，BD = 8，CD = 4，求△DEF的周长.

答案： 解析
(1)
∵∠B = 40°,∠C = 55°,
∴∠BAC = 180° - ∠B - ∠C = 85°,
∵E,F分别为边AC,BC的中点,
∴EF//AB,
∴∠CEF = ∠BAC = 85°,
在Rt△ADC中,E为斜边AC的中点,
∴DE = $\frac{1}{2}$AC = EC,
∴∠EDC = ∠C = 55°,
∴∠DEC = 180° - ∠EDC - ∠C = 70°,
∴∠DEF = 85° - 70° = 15°.
(2)在Rt△ADB中,AD = 6,BD = 8,
由勾股定理得AB = $\sqrt{AD^{2}+BD^{2}}$ = $\sqrt{6^{2}+8^{2}}$ = 10,
∵E,F分别为边AC,BC的中点,
∴EF = $\frac{1}{2}$AB = 5,
在Rt△ADC中,AD = 6,CD = 4,
由勾股定理得AC = $\sqrt{AD^{2}+CD^{2}}$ = $\sqrt{6^{2}+4^{2}}$ = 2$\sqrt{13}$,
∴DE = $\frac{1}{2}$AC = $\sqrt{13}$,
∵BD = 8,CD = 4,
∴BC = 12,
∵F为边BC的中点,
∴CF = 6,
∴DF = 6 - 4 = 2,
∴△DEF的周长 = 5 + 2 + $\sqrt{13}$ = 7 + $\sqrt{13}$.