第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.(2024 湖南长沙长郡教育集团一模)中国航天取得了举世瞩目的成就,为人类科技进步贡献了中国智慧和力量,下列是有关中国航天的图案,其中是中心对称图形的是 ( )


答案:
D 选项 D 中的图案绕某一点旋转 180°后能够与原来的图案重合,所以它是中心对称图形,其他选项均不符合题意,故选 D.
2. [新独家原创] 数学世界奇妙无穷,其中曲线是重要的几何研究对象之一,在一次计算机课上,同学们利用几何画板绘制出了下列曲线,其中不是中心对称图形的是 ( )


答案:
B 由中心对称图形的定义可知,选项 B 不是中心对称图形,故选 B.
3. 跨物理·实验器材(2024 湖南永州祁阳一模)下列图形是物理学中实验器材的平面示意图,从左至右分别代表小车、音叉、凹透镜和砝码,其中既是中心对称图形又是轴对称图形的是 ( )


答案:
C A.不是中心对称图形,是轴对称图形;B.不是中心对称图形,是轴对称图形;C.既是中心对称图形,也是轴对称图形;D.不是中心对称图形,是轴对称图形.故选 C.
4. 小张在美术课上用正方形纸片制作成图 1 的“七巧板”,设计拼成了水杉树树冠(如图 2). 若图 1 中正方形纸片的边长为 2 cm,则图 2 中水杉树树冠的高(即点 A 到线段 BC 的距离)是 ________.


答案:
答案 $(\sqrt{2}+1)\text{cm}$解析 根据题图可知,水杉树树冠的高为题图 1 中正方形边长的一半加上对角线长的一半,$\because$ 题图 1 中正方形边长为 2 cm,$\therefore$ 正方形对角线长为 $2\sqrt{2}\text{ cm}$,$\therefore$ 题图 2 中水杉树树冠的高为 $(\sqrt{2}+1)\text{cm}$.
5. 如图,一艘轮船位于灯塔 P 的南偏东 60°方向,距离灯塔 45 海里的 A 处,它沿北偏东 30°方向航行 60 海里到达 B 处,此时与灯塔 P 的距离为 ( )

A.27 海里
B.50 海里
C.75 海里
D.15$\sqrt{3}$海里

A.27 海里
B.50 海里
C.75 海里
D.15$\sqrt{3}$海里
答案:
C 如图,过点 A 作 $AC// PE$ 交 BP 于点 C,根据题意得 $\angle CAP = \angle EPA = 60^{\circ}$,$\angle CAB = 30^{\circ}$,$PA = 45$ 海里,$AB = 60$ 海里,
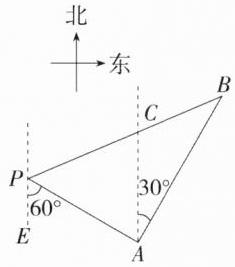
$\therefore \angle PAB = \angle CAP+\angle CAB = 90^{\circ}$,在 $Rt\triangle PAB$ 中,根据勾股定理得 $PB = \sqrt{AP^{2}+AB^{2}}=\sqrt{45^{2}+60^{2}}=\sqrt{5625}=75$(海里),故此时与灯塔 P 的距离为 75 海里.故选 C.
C 如图,过点 A 作 $AC// PE$ 交 BP 于点 C,根据题意得 $\angle CAP = \angle EPA = 60^{\circ}$,$\angle CAB = 30^{\circ}$,$PA = 45$ 海里,$AB = 60$ 海里,

$\therefore \angle PAB = \angle CAP+\angle CAB = 90^{\circ}$,在 $Rt\triangle PAB$ 中,根据勾股定理得 $PB = \sqrt{AP^{2}+AB^{2}}=\sqrt{45^{2}+60^{2}}=\sqrt{5625}=75$(海里),故此时与灯塔 P 的距离为 75 海里.故选 C.
6. 如图,A 市气象站测得台风中心在 A 市正东方向 300 千米的 B 处,以 10$\sqrt{7}$千米/时的速度向北偏西 60°的 BF 方向移动,距台风中心 200 千米范围内是受台风影响的区域. A 市是否会受到台风的影响?若受影响,请求出 A 市受影响的时间;若不受影响,请说明理由.


答案:
解析 A 市会受到台风影响.如图,过点 A 作 $AC\perp BF$ 于点 C,易得 $\angle ABC = 30^{\circ}$,$\therefore AC=\frac{1}{2}AB = 150$ 千米 $<200$ 千米,$\therefore A$ 市会受到台风影响.过点 A 作 $AD = AE = 200$ 千米,交 $BF$ 于点 $D$,$E$,$\therefore DC=\sqrt{AD^{2}-AC^{2}}=\sqrt{200^{2}-150^{2}} = 50\sqrt{7}$(千米).易知 $DC = CE$,$\because$ 台风速度为 $10\sqrt{7}$ 千米/时,$\therefore$ 该市受台风影响的时间为 $\frac{50\sqrt{7}\times2}{10\sqrt{7}} = 10$(小时)

解析 A 市会受到台风影响.如图,过点 A 作 $AC\perp BF$ 于点 C,易得 $\angle ABC = 30^{\circ}$,$\therefore AC=\frac{1}{2}AB = 150$ 千米 $<200$ 千米,$\therefore A$ 市会受到台风影响.过点 A 作 $AD = AE = 200$ 千米,交 $BF$ 于点 $D$,$E$,$\therefore DC=\sqrt{AD^{2}-AC^{2}}=\sqrt{200^{2}-150^{2}} = 50\sqrt{7}$(千米).易知 $DC = CE$,$\because$ 台风速度为 $10\sqrt{7}$ 千米/时,$\therefore$ 该市受台风影响的时间为 $\frac{50\sqrt{7}\times2}{10\sqrt{7}} = 10$(小时)

查看更多完整答案,请扫码查看


