《2025年5年中考3年模拟八年级数学下册湘教版》

9.如图，在Rt△ABC中，CD是斜边AB上的中线，EF经过点C且平行于AB.若∠BCF = 35°，求∠ACD的度数.

答案： 解析 $\because AB// EF,\angle BCF = 35^{\circ},\therefore\angle B=\angle BCF = 35^{\circ}$，$\therefore$在$Rt\triangle ABC$中，$\angle A = 90^{\circ}-\angle B = 55^{\circ}$.$\because CD$是斜边$AB$上的中线，$\therefore AD = BD = CD$，$\therefore\angle ACD=\angle A = 55^{\circ}$.

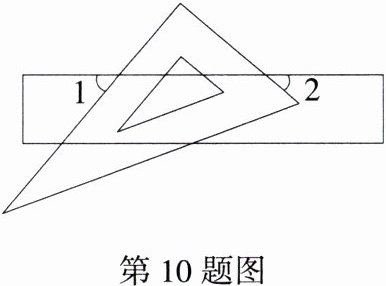
10.(2024黑龙江齐齐哈尔中考,4,★☆☆)将一个含30°角的三角尺和直尺放置如图，若∠1 = 50°，则∠2的度数是(M8201001) （ ）

A.30°
B.40°
C.50°
D.60°

答案：
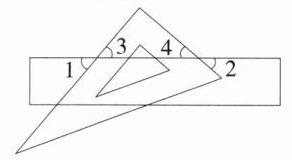
B 如图，$\because\angle 3=\angle 1 = 50^{\circ},\therefore\angle 4 = 90^{\circ}-\angle 3 = 40^{\circ}$，$\therefore\angle 2=\angle 4 = 40^{\circ}$. 故选 B.

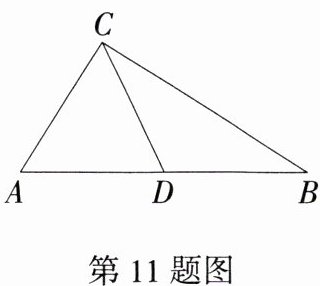
11.(2024广西南宁青秀期中,6,★☆☆)如图，在△ABC中，∠A + ∠B = 90°，AD = DB，CD = 3，则AB的长度为 （ ）

A.3
B.4
C.5
D.6

答案： D $\because$在$\triangle ABC$中，$\angle A+\angle B = 90^{\circ},\therefore\angle ACB = 90^{\circ}$.$\because AD = DB$，$\therefore CD$是该直角三角形斜边$AB$上的中线，$\therefore AB = 2CD = 6$. 故选 D.

12.(2024湖南邵阳新宁月考,8,★☆☆)如图，在四边形ABCD中，∠ABC = ∠ADC = 90°，E为对角线AC的中点，连接BE，DE，若∠BAD = 58°，则∠BED的度数为(M8201001) （ ）

A.118°
B.108°
C.122°
D.116°

答案： D $\because\angle ABC=\angle ADC = 90^{\circ},E$为对角线$AC$的中点，$\therefore ED = AE=\frac{1}{2}AC,EB = AE=\frac{1}{2}AC$，$\therefore\angle ADE=\angle DAE,\angle EAB=\angle ABE$，$\because\angle BAD = 58^{\circ},\therefore\angle DAE+\angle EAB=\angle ADE+\angle ABE = 58^{\circ}$，$\because\angle DEC=\angle DAE+\angle ADE,\angle BEC=\angle ABE+\angle EAB$，$\therefore\angle BED=\angle DEC+\angle BEC=\angle DAE+\angle ADE+\angle ABE+\angle EAB = 116^{\circ}$，故选 D.

13.(2024湖南永州双牌期末,16,★☆☆)如图，在△ABC中，∠A = 35°，∠B = 90°，线段AC的垂直平分线MN与AB交于点D，与AC交于点E，则∠BCD = ________°.

答案： 答案 20\n**解析** 在$\triangle ABC$中，$\because\angle A = 35^{\circ},\angle B = 90^{\circ}$，$\therefore\angle ACB = 90^{\circ}-\angle A = 90^{\circ}-35^{\circ}=55^{\circ}$，$\because MN$是线段$AC$的垂直平分线，$\therefore AD = CD$，$\therefore\angle ACD=\angle A = 35^{\circ}$，$\therefore\angle BCD=\angle ACB-\angle ACD = 55^{\circ}-35^{\circ}=20^{\circ}$.

14.(2024湖南岳阳九中期中,13,★☆☆)如图，BE、CF分别是△ABC中AC、AB边上的高，M为BC的中点，连接FM、EM.若EF = 5，BC = 8，则△EFM的周长是________.

答案： 答案 13\n**解析** $\because BE、CF$分别是$\triangle ABC$中$AC、AB$边上的高，$M$为$BC$的中点，$BC = 8$，$\therefore$在$Rt\triangle BCE$中，$EM=\frac{1}{2}BC = 4$，在$Rt\triangle BCF$中，$FM=\frac{1}{2}BC = 4$，又$\because EF = 5$，$\therefore\triangle EFM$的周长$=EM + FM+EF = 4 + 4+5 = 13$.

15.构造斜边中线法(2024湖南怀化新晃期中,20,★★☆)如图，在△ABC和△ADC中，∠ABC = ∠ADC = 90°，连接BD交AC于点O，M、N分别是AC、BD的中点.求证:MN平分平分BD.

答案：
证明 如图，连接$BM、DM$，
$\because\angle ABC=\angle ADC = 90^{\circ},M$为$AC$的中点，
$\therefore BM=\frac{1}{2}AC,DM=\frac{1}{2}AC$，
$\therefore BM = DM$，
$\because$点$N$是$BD$的中点，
$\therefore MN\perp BD$，$\therefore MN$垂直平分$BD$.