第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.(2024湖南娄底月考)如图,BE = CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需添加一个条件是 ( )

A.AB//CD
B.∠C = ∠B
C.AB = CD
D.∠B = ∠D

A.AB//CD
B.∠C = ∠B
C.AB = CD
D.∠B = ∠D
答案:
C
$\because AE\perp BC,DF\perp BC,\therefore\angle CFD=\angle AEB = 90^{\circ}$,
$\because BE = CF$,$\therefore$当添加$AB = CD$时,根据“HL”可判定$Rt\triangle ABE\cong Rt\triangle DCF$,故选 C.
$\because AE\perp BC,DF\perp BC,\therefore\angle CFD=\angle AEB = 90^{\circ}$,
$\because BE = CF$,$\therefore$当添加$AB = CD$时,根据“HL”可判定$Rt\triangle ABE\cong Rt\triangle DCF$,故选 C.
2.如图所示,在△ABC中,AB = CB,∠ABC = 90°,F为AB延长线上一点,点E在BC上,且AE = CF.
求证:Rt△ABE≌Rt△CBF.(M8201004)

求证:Rt△ABE≌Rt△CBF.(M8201004)

答案:
证明
$\because\angle ABC = 90^{\circ},\therefore\angle CBF = 90^{\circ}$,
在$Rt\triangle ABE$和$Rt\triangle CBF$中,$\begin{cases}AE = CF,\\AB = CB,\end{cases}$
$\therefore Rt\triangle ABE\cong Rt\triangle CBF(HL)$.
$\because\angle ABC = 90^{\circ},\therefore\angle CBF = 90^{\circ}$,
在$Rt\triangle ABE$和$Rt\triangle CBF$中,$\begin{cases}AE = CF,\\AB = CB,\end{cases}$
$\therefore Rt\triangle ABE\cong Rt\triangle CBF(HL)$.
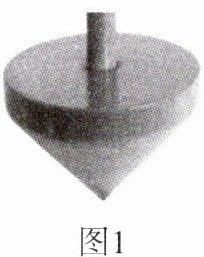
3.新独家原创 陀螺在我国有上千年的历史.传统陀螺大致是由木或铁制成的倒圆锥形,玩法是用鞭子抽打,流传甚广.图1是一个木制的陀螺,图2是其轴剖面示意图,已知AB = BC,∠BAD = ∠BCD = 90°,点D是EF上一点,AE⊥EF于点E,CF⊥EF于点F,DE = DF,连接BD,
求证:AE = CF.

求证:AE = CF.


答案:
证明
在$Rt\triangle ABD$和$Rt\triangle CBD$中,$\begin{cases}BD = BD,\\AB = CB,\end{cases}$
$\therefore Rt\triangle ABD\cong Rt\triangle CBD(HL)$,$\therefore AD = CD$,
$\because AE\perp EF$于点$E,CF\perp EF$于点$F$,
$\therefore\angle E=\angle F = 90^{\circ}$,
在$Rt\triangle ADE$和$Rt\triangle CDF$中,$\begin{cases}AD = CD,\\DE = DF,\end{cases}$
$\therefore Rt\triangle ADE\cong Rt\triangle CDF(HL)$,$\therefore AE = CF$.
在$Rt\triangle ABD$和$Rt\triangle CBD$中,$\begin{cases}BD = BD,\\AB = CB,\end{cases}$
$\therefore Rt\triangle ABD\cong Rt\triangle CBD(HL)$,$\therefore AD = CD$,
$\because AE\perp EF$于点$E,CF\perp EF$于点$F$,
$\therefore\angle E=\angle F = 90^{\circ}$,
在$Rt\triangle ADE$和$Rt\triangle CDF$中,$\begin{cases}AD = CD,\\DE = DF,\end{cases}$
$\therefore Rt\triangle ADE\cong Rt\triangle CDF(HL)$,$\therefore AE = CF$.
4.如图,∠C = ∠D = 90°,添加下列哪个条件,一定能判定Rt△ABC≌Rt△ABD(M8201004) ( )
①AC = AD;
②∠ABC = ∠ABD;
③BC = BD;
④∠BAC = ∠BAD.

A.①②③
B.①③
C.①③④
D.①②③④
①AC = AD;
②∠ABC = ∠ABD;
③BC = BD;
④∠BAC = ∠BAD.

A.①②③
B.①③
C.①③④
D.①②③④
答案:
D
①当$AC = AD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(HL)$;
②当$\angle ABC=\angle ABD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(AAS)$;
③当$BC = BD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(HL)$;
④当$\angle BAC=\angle BAD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(AAS)$.
综上,①②③④均符合题意,故选 D.
①当$AC = AD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(HL)$;
②当$\angle ABC=\angle ABD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(AAS)$;
③当$BC = BD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(HL)$;
④当$\angle BAC=\angle BAD$时,由$\angle C=\angle D = 90^{\circ}$,且$AB = AB$,可得$Rt\triangle ABC\cong Rt\triangle ABD(AAS)$.
综上,①②③④均符合题意,故选 D.
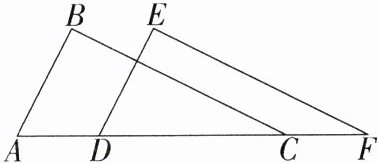
5.如图,点A、D、C、F在同一条直线上,∠B = ∠E = 90°,AD = CF,BC = EF.(M8201004)
(1)求证:Rt△ABC≌Rt△DEF.
(2)若∠A = 50°,求∠F的度数.
(1)求证:Rt△ABC≌Rt△DEF.
(2)若∠A = 50°,求∠F的度数.

答案:
解析
(1) 证明:$\because AC = AD + DC,DF = DC + CF$,且$AD = CF$,$\therefore AC = DF$,
在$Rt\triangle ABC$和$Rt\triangle DEF$中,$\begin{cases}AC = DF,\\BC = EF,\end{cases}$
$\therefore Rt\triangle ABC\cong Rt\triangle DEF(HL)$.
(2)$\because\angle B = 90^{\circ},\angle A = 50^{\circ},\therefore\angle BCA = 40^{\circ}$,
由
(1)知$Rt\triangle ABC\cong Rt\triangle DEF$,
$\therefore\angle F=\angle BCA = 40^{\circ}$.
(1) 证明:$\because AC = AD + DC,DF = DC + CF$,且$AD = CF$,$\therefore AC = DF$,
在$Rt\triangle ABC$和$Rt\triangle DEF$中,$\begin{cases}AC = DF,\\BC = EF,\end{cases}$
$\therefore Rt\triangle ABC\cong Rt\triangle DEF(HL)$.
(2)$\because\angle B = 90^{\circ},\angle A = 50^{\circ},\therefore\angle BCA = 40^{\circ}$,
由
(1)知$Rt\triangle ABC\cong Rt\triangle DEF$,
$\therefore\angle F=\angle BCA = 40^{\circ}$.
6.教材变式·P21T4 下面是小东设计的“已知两线段,求作直角三角形”的尺规作图完整过程.
已知:如图1,线段a及线段b(a < b).
求作:Rt△ABC,使得a、b分别为它的一条直角边和斜边.
作法:如图2,
①作射线CM,在CM上顺次截取CB = BD = a;
②分别以点C、D为圆心,以b的长为半径画弧,两弧交于点A;
③连接AB、AC,则△ABC就是所求作的直角三角形.
根据小东设计的尺规作图过程,回答下列问题:
(1)补全图形,保留作图痕迹.
(2)完成下面的证明.
证明:连接AD,
∵ ______ = AD,CB = ______,
∴ ∠ABC = 90°( ____________ )(填推理依据).
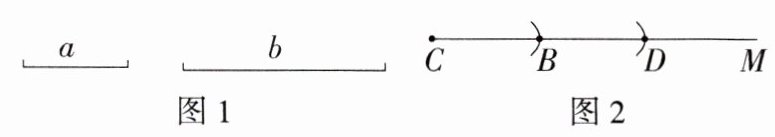
已知:如图1,线段a及线段b(a < b).
求作:Rt△ABC,使得a、b分别为它的一条直角边和斜边.
作法:如图2,
①作射线CM,在CM上顺次截取CB = BD = a;
②分别以点C、D为圆心,以b的长为半径画弧,两弧交于点A;
③连接AB、AC,则△ABC就是所求作的直角三角形.
根据小东设计的尺规作图过程,回答下列问题:
(1)补全图形,保留作图痕迹.
(2)完成下面的证明.
证明:连接AD,
∵ ______ = AD,CB = ______,
∴ ∠ABC = 90°( ____________ )(填推理依据).
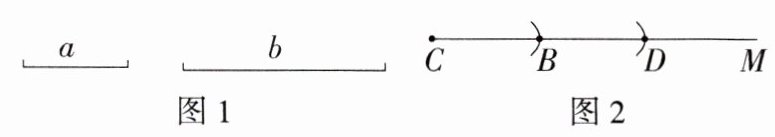
答案:
解析
(1) 如图所示.
(2)$AC$;$BD$;等腰三角形的三线合一.
解析
(1) 如图所示.

(2)$AC$;$BD$;等腰三角形的三线合一.
查看更多完整答案,请扫码查看


