第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1. 下图是一个三级台阶的示意图,每一级的长、宽、高分别为 9、3、1,A 和 B 是这个台阶两个相对的点,A 点有一只蚂蚁,想到 B 点去吃可口的食物,则这只蚂蚁沿着台阶面爬行的最短路程是 ( )
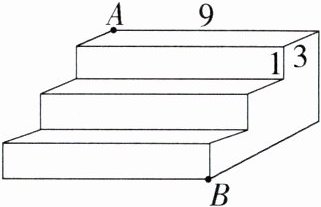
A. 18
B. 15
C. 12
D. 8

A. 18
B. 15
C. 12
D. 8
答案:
B 如图,将台阶面展开,连接 $AB$,线段 $AB$ 即为蚂蚁所爬行的最短路线。
由题意得 $AC = 3×3 + 1×3 = 12$,$BC = 9$,
$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{12^{2}+9^{2}} = 15$,
$\therefore$ 这只蚂蚁爬行的最短路程为 $15$。故选 B。

B 如图,将台阶面展开,连接 $AB$,线段 $AB$ 即为蚂蚁所爬行的最短路线。
由题意得 $AC = 3×3 + 1×3 = 12$,$BC = 9$,
$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{12^{2}+9^{2}} = 15$,
$\therefore$ 这只蚂蚁爬行的最短路程为 $15$。故选 B。

2.(2023 四川广安中考,15)如图,圆柱形玻璃杯的杯高为 9 cm,底面周长为 16 cm,在杯内壁离杯底 4 cm 的点 A 处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿 1 cm,且与蜂蜜相对的点 B 处,则蚂蚁从外壁 B 处到内壁 A 处所走的最短路程为 ________ cm.(杯壁厚度不计)
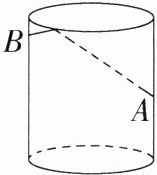

答案:
答案 $10$
解析 如图,将玻璃杯侧面展开(展开图的一半),作 $B$ 关于 $EF$ 的对称点 $B'$,作 $B'D\perp AE$,交 $AE$ 的延长线于点 $D$,连接 $AB'$,
由题意得 $DE=\frac{1}{2}BB' = 1\ cm$,$AE = 9 - 4 = 5(cm)$,
$\therefore AD = AE + DE = 6\ cm$,
$\because$ 玻璃杯底面周长为 $16\ cm$,
$\therefore B'D=\frac{1}{2}×16 = 8(cm)$,$\therefore AB'=\sqrt{AD^{2}+B'D^{2}} = 10\ cm$,
由两点之间线段最短可知,蚂蚁从外壁 $B$ 处到内壁 $A$ 处所走的最短路程为 $AB' = 10\ cm$。
故答案为 $10$。
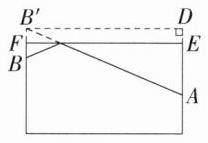
答案 $10$
解析 如图,将玻璃杯侧面展开(展开图的一半),作 $B$ 关于 $EF$ 的对称点 $B'$,作 $B'D\perp AE$,交 $AE$ 的延长线于点 $D$,连接 $AB'$,
由题意得 $DE=\frac{1}{2}BB' = 1\ cm$,$AE = 9 - 4 = 5(cm)$,
$\therefore AD = AE + DE = 6\ cm$,
$\because$ 玻璃杯底面周长为 $16\ cm$,
$\therefore B'D=\frac{1}{2}×16 = 8(cm)$,$\therefore AB'=\sqrt{AD^{2}+B'D^{2}} = 10\ cm$,
由两点之间线段最短可知,蚂蚁从外壁 $B$ 处到内壁 $A$ 处所走的最短路程为 $AB' = 10\ cm$。
故答案为 $10$。

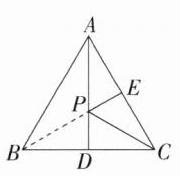
3. 在等边三角形 ABC 中,D 是 BC 的中点,点 E,P 分别是线段 AC,AD 上的动点,已知 AB = 2,求 PE + PC 的最小值.
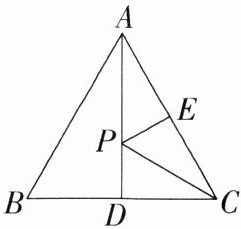

答案:
解析 如图,过 $B$ 作 $BE\perp AC$ 于 $E$,与 $AD$ 交于点 $P$,连接 $PC$,此时 $PE + PC$ 的值最小,
$\because\triangle ABC$ 是等边三角形,$D$ 为 $BC$ 的中点,
$\therefore AD$ 垂直平分 $BC$,$\therefore PC = PB$,
$\therefore PE + PC = PE + PB = BE$,
即 $BE$ 的长就是 $PE + PC$ 的最小值,
$\because\triangle ABC$ 是一个边长为 $2$ 的等边三角形,$BE\perp AC$,
$\therefore\angle BEC = 90^{\circ}$,$CE = 1$,$\therefore BE=\sqrt{BC^{2}-CE^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
$\therefore PE + PC$ 的最小值是 $\sqrt{3}$。
解析 如图,过 $B$ 作 $BE\perp AC$ 于 $E$,与 $AD$ 交于点 $P$,连接 $PC$,此时 $PE + PC$ 的值最小,
$\because\triangle ABC$ 是等边三角形,$D$ 为 $BC$ 的中点,
$\therefore AD$ 垂直平分 $BC$,$\therefore PC = PB$,
$\therefore PE + PC = PE + PB = BE$,
即 $BE$ 的长就是 $PE + PC$ 的最小值,
$\because\triangle ABC$ 是一个边长为 $2$ 的等边三角形,$BE\perp AC$,
$\therefore\angle BEC = 90^{\circ}$,$CE = 1$,$\therefore BE=\sqrt{BC^{2}-CE^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
$\therefore PE + PC$ 的最小值是 $\sqrt{3}$。

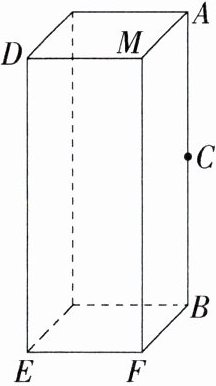
4. 转化法 如图,一个长方体盒子的长(EF)、宽(BF)、高(MF)分别是 12 cm、8 cm、30 cm,在 AB 的中点 C 处有一滴蜂蜜,一只小虫从 E 处沿盒子表面爬到 C 处去吃,求小虫爬行的最短路程.

答案:
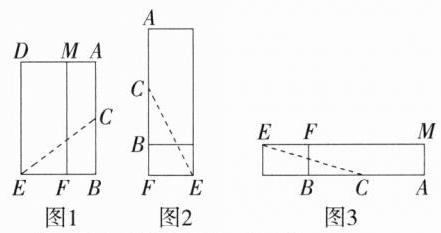
解析 分三种情况:
①如图 1,连接 $EC$。
在 $Rt\triangle EBC$ 中,$EB = 12 + 8 = 20(cm)$,$BC=\frac{1}{2}×30 = 15(cm)$,由勾股定理,得 $EC=\sqrt{EB^{2}+BC^{2}}=\sqrt{20^{2}+15^{2}} = 25(cm)$。
②如图 2,连接 $EC$。
同理可得 $CE=\sqrt{EF^{2}+FC^{2}}=\sqrt{12^{2}+(8 + 15)^{2}}=\sqrt{673}\ cm>25\ cm$。
③如图 3,连接 $EC$。
同理可得 $CE=\sqrt{8^{2}+(12 + 15)^{2}}=\sqrt{793}\ cm>25\ cm$。
综上可知,小虫爬行的最短路程是 $25\ cm$。
解析 分三种情况:
①如图 1,连接 $EC$。
在 $Rt\triangle EBC$ 中,$EB = 12 + 8 = 20(cm)$,$BC=\frac{1}{2}×30 = 15(cm)$,由勾股定理,得 $EC=\sqrt{EB^{2}+BC^{2}}=\sqrt{20^{2}+15^{2}} = 25(cm)$。
②如图 2,连接 $EC$。
同理可得 $CE=\sqrt{EF^{2}+FC^{2}}=\sqrt{12^{2}+(8 + 15)^{2}}=\sqrt{673}\ cm>25\ cm$。
③如图 3,连接 $EC$。
同理可得 $CE=\sqrt{8^{2}+(12 + 15)^{2}}=\sqrt{793}\ cm>25\ cm$。
综上可知,小虫爬行的最短路程是 $25\ cm$。

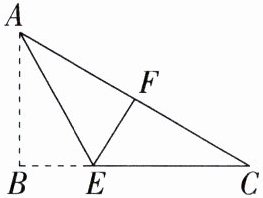
5. 如图,在 Rt△ABC 中,∠ABC = 90°,点 E 在 BC 边上,将△ABE 沿 AE 折叠,使点 B 恰好落在斜边 AC 上的点 F 处.
(1)若 AE = CE,求∠C 的度数.
(2)若 AB = 3,BC = 4,求△CEF 的周长.
(1)若 AE = CE,求∠C 的度数.
(2)若 AB = 3,BC = 4,求△CEF 的周长.

答案:
解析
(1) 由折叠的性质可得 $\angle BAE=\angle CAE$,
$\because AE = CE$,$\therefore\angle C=\angle CAE$。
$\because\angle C+\angle BAC = 90^{\circ}$,$\therefore\angle C+\angle BAE+\angle CAE = 90^{\circ}$,
$\therefore 3\angle C = 90^{\circ}$,$\therefore\angle C = 30^{\circ}$。
(2) $\because$ 在 $Rt\triangle ABC$ 中,$\angle ABC = 90^{\circ}$,$AB = 3$,$BC = 4$,
$\therefore AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$,
由折叠的性质可得 $AF = AB = 3$,$EF = BE$,
$\therefore CF = AC - AF = 2$,$\therefore\triangle CEF$ 的周长为 $CE + EF + CF = CE + BE + CF = BC + CF = 4 + 2 = 6$。
(1) 由折叠的性质可得 $\angle BAE=\angle CAE$,
$\because AE = CE$,$\therefore\angle C=\angle CAE$。
$\because\angle C+\angle BAC = 90^{\circ}$,$\therefore\angle C+\angle BAE+\angle CAE = 90^{\circ}$,
$\therefore 3\angle C = 90^{\circ}$,$\therefore\angle C = 30^{\circ}$。
(2) $\because$ 在 $Rt\triangle ABC$ 中,$\angle ABC = 90^{\circ}$,$AB = 3$,$BC = 4$,
$\therefore AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$,
由折叠的性质可得 $AF = AB = 3$,$EF = BE$,
$\therefore CF = AC - AF = 2$,$\therefore\triangle CEF$ 的周长为 $CE + EF + CF = CE + BE + CF = BC + CF = 4 + 2 = 6$。
查看更多完整答案,请扫码查看


