《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

10. 在Rt△ABC中，∠C = 90°，请根据下面的条件解直角三角形.
（1）BC = 8，∠B = 60°； （2）AC = $\sqrt{2}$，AB = 2.

答案：
(1) $\angle A = 30^{\circ}$，$AB = 16$，$AC = 8\sqrt{3}$
(2) $\angle A=\angle B = 45^{\circ}$，$BC=\sqrt{2}$

11. （2024·滨州改编）在锐角三角形ABC中，∠A、∠B、∠C的对边分别为a、b、c，边、角总满足关系式：$\frac{a}{sinA}$ = $\frac{b}{sinB}$ = $\frac{c}{sinC}$.
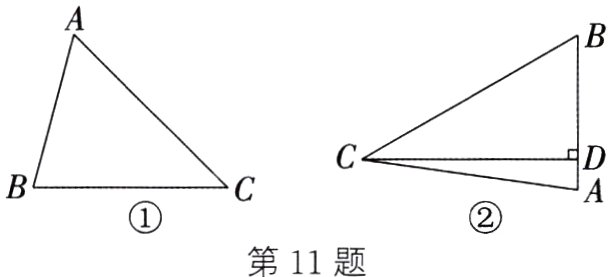
（1）如图①，若∠B = 75°，∠C = 45°，BC = 2，求AB的长.
（2）如图②，某公园准备在园内一个锐角三角形水池ABC中建一座小型景观桥CD. 若CD⊥AB，AC = 14 m，AB = 10 m，sin∠ACB = $\frac{5\sqrt{3}}{14}$，求景观桥CD的长度.
　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案：
(1) $\because$在$\triangle ABC$中，$\angle B = 75^{\circ}$，$\angle C = 45^{\circ}$，$\therefore\angle A = 60^{\circ}$。$\because BC = 2$，$\frac{BC}{\sin A}=\frac{AB}{\sin C}$，$\therefore\frac{2}{\sin60^{\circ}}=\frac{AB}{\sin45^{\circ}}$。$\therefore AB=\sin45^{\circ}\times\frac{2}{\sin60^{\circ}}=\frac{\sqrt{2}}{2}\times\frac{2}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{6}}{3}$
(2) $\because$在$\triangle ABC$中，$\frac{AB}{\sin\angle ACB}=\frac{AC}{\sin B}$，$\therefore\frac{10}{\frac{5\sqrt{3}}{14}}=\frac{14}{\sin B}$。$\therefore\sin B=\frac{\sqrt{3}}{2}$。$\therefore\angle B = 60^{\circ}$。设$BD = x$m$(x\gt0)$，则$AD=(10 - x)$m，$CD = BD\cdot\tan60^{\circ}=\sqrt{3}x$m。在$Rt\triangle ADC$中，由勾股定理，得$CD^{2}+AD^{2}=AC^{2}$，即$(\sqrt{3}x)^{2}+(10 - x)^{2}=14^{2}$。化简，得$x^{2}-5x - 24 = 0$，解得$x_{1}=-3$(不合题意，舍去)，$x_{2}=8$。$\therefore\sqrt{3}x = 8\sqrt{3}$。$\therefore$景观桥$CD$的长度为$8\sqrt{3}$m

12. （2023·南充改编）如图，为了测量一条河流的宽度，测量员在河岸边相距200 m的P、Q两点分别测对岸点T的位置，点T在点P的正北方向，在点Q的北偏西70°方向，则这条河流的宽度（PT的长）为 （ ）
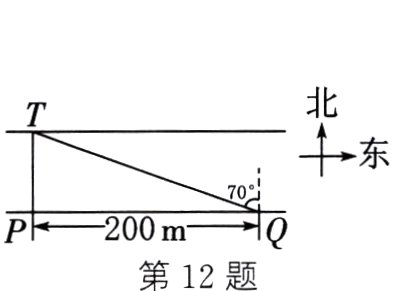
A. 200tan70° m B. $\frac{200}{tan70°}$ m C. 200sin70° m D. $\frac{200}{sin70°}$ m
　　　　　　　　　　

答案： B

13. 大坝的横截面是等腰梯形，其上底与腰的夹角是135°，则坝坡的坡度是_______.

答案： 1:1

14. （2024·德阳）如图，某校学生开展综合实践活动，测量一建筑物CD的高度，在建筑物旁边有一高度为10 m的小楼房AB，小李同学在小楼房楼底B处测得C处的仰角为60°，在小楼房楼顶A处测得C处的仰角为30°（AB、CD在同一平面内，点B、D在同一水平面上），则建筑物CD的高为_______m.

答案： 15