《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

3. (2023·常德)如图①，在Rt△ABC中，∠ABC=90°，AB=8，BC=6，D是AB上一点，且AD=2，过点D作DE//BC交AC于点E. 将△ADE绕点A按顺时针方向旋转到图②的位置，连接BD、CE，则图②中$\frac{BD}{CE}$的值为__________:
　　　　　　　　　　　　　　

答案： $\frac{4}{5}$ 解析：
∵ ∠ABC = 90°，AB = 8，BC = 6，
∴ AC = $\sqrt{AB^{2}+BC^{2}}=\sqrt{8^{2}+6^{2}} = 10$.
∵ DE//BC，
∴ △ADE∽△ABC.
∴ $\frac{AD}{AB}=\frac{AE}{AC}$，即$\frac{AD}{AE}=\frac{AB}{AC}$.
∵ 将△ADE绕点A按顺时针方向旋转到题图②的位置，
∴ ∠DAB = ∠EAC.
∴ △ADB∽△AEC.
∴ $\frac{BD}{CE}=\frac{AB}{AC}=\frac{8}{10}=\frac{4}{5}$.

4. 小王学习了相似图形后，进一步开展探究活动：将一个矩形ABCD绕点A按顺时针方向旋转α(0°＜α≤90°)，得到矩形AB'C'D'，连接BD.
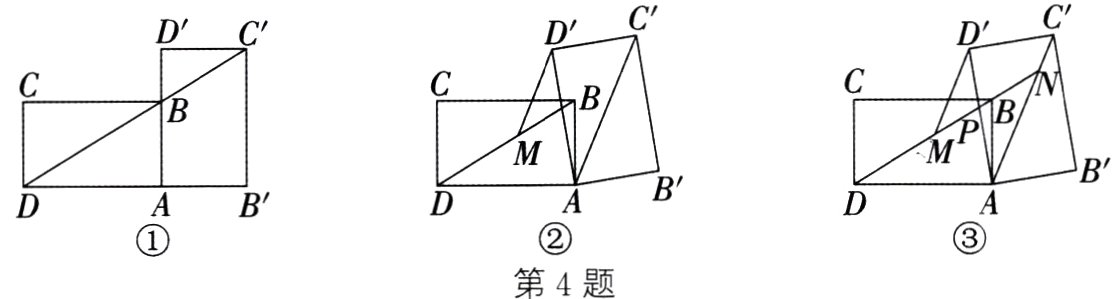
　(1) 如图①，当α=90°时，点C'恰好在线段DB的延长线上. 若AB=1，求BC的长.
　(2) 如图②，连接AC'，过点D'作D'M//AC'，交BD于点M. 线段DM与D'M的长相等吗？请说明理由.
　　(3) 如图③，在(2)的条件下，射线DB分别交AD'、AC'于点P、N，小王发现线段DN、MN、PN之间存在一定的数量关系，请写出这个关系式，并加以证明.
　　　　　　　　

答案： （1）设BC = x.
∵ 将矩形ABCD绕点A按顺时针方向旋转90°，得到矩形AB'C'D'，
∴ 点A、B、D'在同一条直线上，AD' = AD = BC = x，D'C' = AB' = AB = 1，∠BAD = ∠D' = 90°.
∴ D'B = AD' - AB = x - 1，D'C'//DA. 又
∵ 点C'在线段DB的延长线上，
∴ ∠D'C'B = ∠ADB.
∴ △D'C'B∽△ADB.
∴ $\frac{D'C'}{AD}=\frac{D'B}{AB}$.
∴ $\frac{1}{x}=\frac{x - 1}{1}$，解得$x_{1}=\frac{1+\sqrt{5}}{2}$，$x_{2}=\frac{1 - \sqrt{5}}{2}$（不合题意，舍去），即BC = $\frac{1+\sqrt{5}}{2}$
（2）DM = D'M 理由：连接DD'.
∵ D'M//AC'，
∴ ∠AD'M = ∠D'AC'. 由题意，易得AD' = DA，∠AD'C' = ∠DAB = 90°，D'C' = AB，
∴ △AC'D'≌△DBA.
∴ ∠D'AC' = ∠ADB.
∴ ∠ADB = ∠AD'M.
∵ AD = AD'，
∴ ∠ADD' = ∠AD'D.
∴ ∠ADD' - ∠ADB = ∠AD'D - ∠AD'M.
∴ ∠MDD' = ∠MD'D.
∴ DM = D'M.
（3）MN² = PN·DN 连接AM.
∵ D'M = DM，AD' = AD，AM = AM，
∴ △AD'M≌△ADM.
∴ ∠MAD' = ∠MAD.
∵ ∠AMN = ∠MAD + ∠NDA，∠NAM = ∠MAD' + ∠NAP，
∴ ∠AMN = ∠NAM.
∴ MN = AN.
∵ ∠ANP = ∠DNA，∠NAP = ∠NDA，
∴ △NAP∽△NDA.
∴ $\frac{PN}{AN}=\frac{AN}{DN}$.
∴ AN² = PN·DN.
∴ MN² = PN·DN