《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

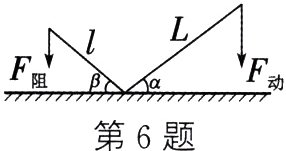
6. 如图，撬钉子的工具是一个杠杆，动力臂L₁ = L·cos α，阻力臂L₂ = l·cos β. 若动力F的用力方向始终保持竖直向下，则当阻力不变时，杠杆向下运动时的动力变化情况是 （ ）
A. 越来越小 B. 不变 C. 越来越大 D. 无法确定
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： A

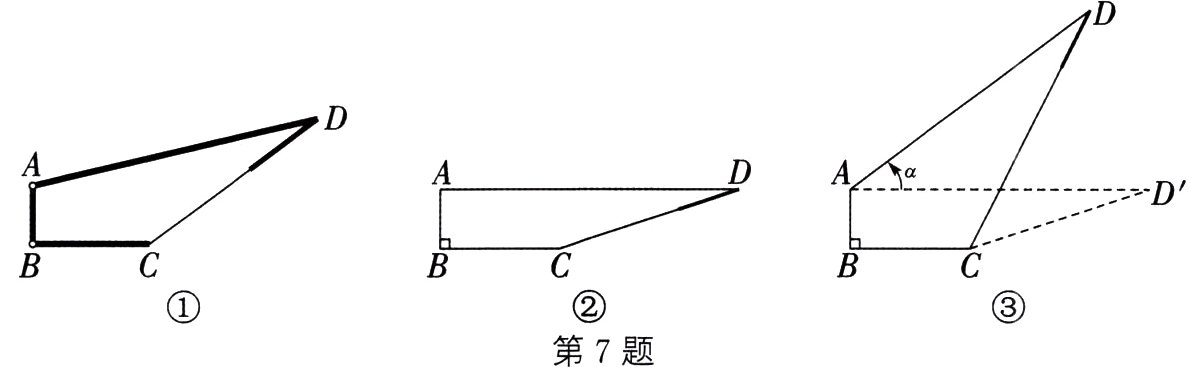
7. （2024·苏州）如图①所示为某种可调节支撑架，BC为水平固定杆，竖直固定杆AB⊥BC，活动杆AD可绕点A旋转，CD为液压可伸缩支撑杆，已知AB = 10 cm，BC = 20 cm，AD = 50 cm.
（1）如图②，当活动杆AD处于水平状态时，可伸缩支撑杆CD的长为________ cm；
（2）如图③，当活动杆AD绕点A由水平状态按逆时针方向旋转角度α，且tan α = $\frac{3}{4}$（α为锐角），则此时可伸缩支撑杆CD的长为________ cm.
　　　　　　

答案：

(1) 10$\sqrt{10}$ 解析：过点C作CE⊥AD，垂足为E. 由题意，得AB = CE = 10 cm，BC = AE = 20 cm，
∵AD = 50 cm，
∴ED = AD - AE = 50 - 20 = 30(cm).
∴在Rt△CED中，由勾股定理，得CD = $\sqrt{CE^{2}+DE^{2}}$ = $\sqrt{10^{2}+30^{2}}$ = 10$\sqrt{10}$(cm).
∴可伸缩支撑杆CD的长为10$\sqrt{10}$cm.
(2) 20$\sqrt{5}$ 解析：如图，过点D作DF⊥BC，交BC的延长线于点F，交AD'于点G. 由题意，得AB = FG = 10 cm，AG = BF，∠AGD = 90°.
∵在Rt△ADG中，tanα = $\frac{DG}{AG}$ = $\frac{3}{4}$，
∴设DG = 3x cm，则AG = 4x cm.
∴在Rt△AGD中，由勾股定理，得AD = $\sqrt{AG^{2}+DG^{2}}$ = 5x cm.
∵AD = 50 cm，
∴5x = 50，解得x = 10.
∴AG = 40 cm，DG = 30 cm.
∴DF = DG + FG = 30 + 10 = 40(cm)，BF = AG = 40 cm.
∵BC = 20 cm，
∴CF = BF - BC = 40 - 20 = 20(cm).
∴在Rt△CFD中，由勾股定理，得CD = $\sqrt{CF^{2}+DF^{2}}$ = $\sqrt{20^{2}+40^{2}}$ = 20$\sqrt{5}$(cm).
∴此时可伸缩支撑杆CD的长为20$\sqrt{5}$cm.

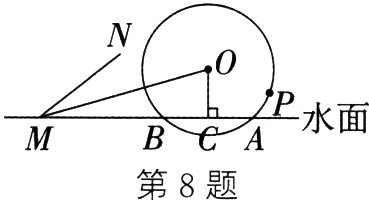
8. （2023·湘潭改编）如图所示为我国古代利用水力驱动的灌溉工具“筒车”的平面示意图. 半径为3 m的筒车☉O按逆时针方向每分钟转$\frac{5}{6}$圈，筒车与水面分别交于点A、B，筒车的轴心O距离水面的高度OC为2.2 m，筒车上均匀分布着若干个盛水筒，以某个盛水筒P刚浮出水面时开始计算时间（参考数据：cos 43° = sin 47°≈$\frac{11}{15}$，sin 16° = cos 74°≈$\frac{11}{40}$，sin 22° = cos 68°≈$\frac{3}{8}$）.
（1）经过________ s，盛水筒P首次到达最高点.
（2）浮出水面3.4 s时，盛水筒P距离水面多高？
（3）若接水槽MN所在直线是☉O的切线，且与直线AB交于点M，MO = 8 m，则盛水筒P从最高点开始，至少经过多长时间恰好在直线MN上？
　

答案：

(1) 27.4 解析：如图①，连接OA. 由题意，得筒车每秒旋转360°×$\frac{5}{6}$÷60 = 5°.
∵在Rt△ACO中，cos∠AOC = $\frac{OC}{OA}$ = $\frac{2.2}{3}$ = $\frac{11}{15}$.
∴∠AOC≈43°.
∴盛水筒P首次到达最高点所需时间为$\frac{180° - 43°}{5°}$ = 27.4(s).
(2) 如图①，连接OP，过点P作PD⊥OC于点D，盛水筒P浮出水面3.4 s时，∠AOP = 3.4×5° = 17°，
∴∠POC = ∠AOC + ∠AOP = 43° + 17° = 60°. 在Rt△POD中，OD = OP·cos60° = 3×$\frac{1}{2}$ = 1.5(m)，
∴浮出水面3.4 s时，盛水筒P距离水面2.2 - 1.5 = 0.7(m)
(3) 如图②，延长CO交⊙O于点H.
∵点P在⊙O上，且MN与⊙O相切，
∴当点P在直线MN上时，P是切点. 延长MN与⊙O交于点P，连接OP，则OP⊥MN.
∵在Rt△OPM中，cos∠POM = $\frac{OP}{OM}$ = $\frac{3}{8}$，
∴∠POM≈68°.
∵在Rt△COM中，cos∠COM = $\frac{OC}{OM}$ = $\frac{2.2}{8}$ = $\frac{11}{40}$，
∴∠COM≈74°.
∴∠POH = 180° - ∠POM - ∠COM = 180° - 68° - 74° = 38°.
∴需要的时间为$\frac{38°}{5°}$ = 7.6(s).
∴盛水筒P从最高点开始，至少经过7.6 s恰好在直线MN上