《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

8. 如图，在6×6的正方形网格中，△ABC的顶点A、B、C都在网格线上，且都是小正方形边的中点，则sinA的值为_______.
　　　　　　　　

答案： $\frac{4}{5}$

9. 如图，在△ABC中，∠ACB = 90°，D为边AB的中点，连接CD. 若BC = 4，CD = 3，则cos∠DCB的值为_______.
　　　　　　　

答案： $\frac{2}{3}$

10. 如图，在Rt△ABC中，∠BAC = 90°，斜边BC上的高AD = 8，sin B = $\frac{3}{5}$，则AC的长为_______.
　　　　　　　

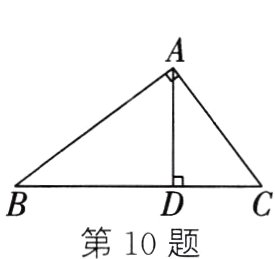
答案： 10 解析：先利用同角的余角相等说明$\angle B = \angle DAC$，即$\sin B = \sin\angle DAC$，即$\frac{DC}{AC} = \frac{3}{5}$，由此可设$DC = 3k(k ＞ 0)$，则$AC = 5k$，在$Rt\triangle ADC$中，根据勾股定理，得$AD = 4k$. $\because AD = 8$，$\therefore 4k = 8$，解得$k = 2$. $\therefore AC = 5\times2 = 10$.

11.（2024·上海）在□ABCD中，∠ABC是锐角，将CD沿直线l翻折至AB所在直线，点C、D的对应点分别为C′、D′. 若AC′：AB：BC = 1：3：7，则cos∠ABC的值为_______.

答案： $\frac{2}{7}$或$\frac{4}{7}$ 解析：分点$C$在线段$AB$上和点$C$在$BA$的延长线上两种情况讨论.

12.（2023·深圳）如图，在菱形ABCD中，cos A = $\frac{1}{3}$，过点C作CE⊥AB，交AB的延长线于点E，过点E作EF⊥AD，交AD于点F. 若$S_{菱形ABCD}=24$，求EF·BC的值.
　　　　　

答案： $\because$ 四边形$ABCD$是菱形，$\therefore AD// BC$，$AB = BC$. $\therefore \angle CBE = \angle A$. $\because \cos A = \frac{1}{3}$，$\therefore \cos\angle CBE = \frac{1}{3}$. $\because CE\perp AB$，$\therefore \angle CEB = 90^{\circ}$. $\therefore$ 在$Rt\triangle CEB$中，$\cos\angle CBE = \frac{BE}{BC} = \frac{1}{3}$. $\therefore BE = \frac{1}{3}BC$. $\therefore AE = AB + BE = AB + \frac{1}{3}BC = AB + \frac{1}{3}AB = \frac{4}{3}AB$. $\because EF\perp AD$，$CE\perp AB$，$\therefore \angle AFE = \angle BEC = 90^{\circ}$. $\therefore \triangle AFE\backsim\triangle BEC$. $\therefore \frac{AE}{BC} = \frac{EF}{CE}$. $\therefore EF\cdot BC = AE\cdot CE = \frac{4}{3}AB\cdot CE = \frac{4}{3}S_{菱形ABCD} = \frac{4}{3}\times24 = 32$

13.（2024·遂宁）小明的书桌上有一个L型台灯，灯柱AB高40 cm，他发现当灯带BC与水平线BM的夹角为9°时（如图①），灯带的直射宽度DE（BD⊥BC，CE⊥BC）为35 cm，但此时灯的直射宽度不够，当他把灯带调整到与水平线夹角为30°时（如图②），直射宽度刚好合适，求此时台灯最高点C到桌面的距离（精确到0.1 cm，参考数据：sin 9°≈0.16，cos 9°≈0.99，sin 30° = 0.5，cos 30°≈0.87）.
　　

答案：
在题图①中，$\because DB\perp BC$，$EC\perp BC$，$\therefore BD// EC$. $\because BM// DE$，$\therefore$ 四边形$BDEM$是平行四边形. $\therefore BM = DE = 35\ cm$. $\because CE\perp BC$，$\therefore$ 在$Rt\triangle BCM$中，$BC = BM\cdot\cos 9^{\circ}\approx 35\times0.99 = 34.65(cm)$. 如图，过点$C$作$CK\perp AE'$于点$K$，交$BM$于点$J$，则四边形$BAKJ$为矩形. $\therefore BA = JK = 40\ cm$，$\angle BJK = \angle BJC = 90^{\circ}$. $\therefore$ 在$Rt\triangle BJC$中，$CJ = BC\cdot\sin 30^{\circ} = 17.325\ cm$. $\therefore CK = CJ + JK = 17.325 + 40\approx 57.3(cm)$. $\therefore$ 台灯最高点$C$到桌面的距离约为$57.3\ cm$