《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

1.（2024·广州）为了解公园用地面积x（单位：公顷）的基本情况，某地随机调查了本地50个公园的用地面积，按照0＜x≤4、4＜x≤8、8＜x≤12、12＜x≤16、16＜x≤20的分组绘制了如图所示的频数分布直方图.下列说法正确的是 （ ）
A. a的值为20
B. 用地面积在8＜x≤12这一组的公园个数最多
C. 用地面积在4＜x≤8这一组的公园个数最少
D. 这50个公园中有一半以上的公园用地面积超过12公顷
　　　　　 　　　　

答案： B

2. 某工厂一共有1200人，为选拔人才，提出了一些选拔的条件，并进行了抽样调查.从中抽出400人，发现有300人是符合条件的，估计该工厂1200人中符合选拔条件的人数为________.

答案： 900

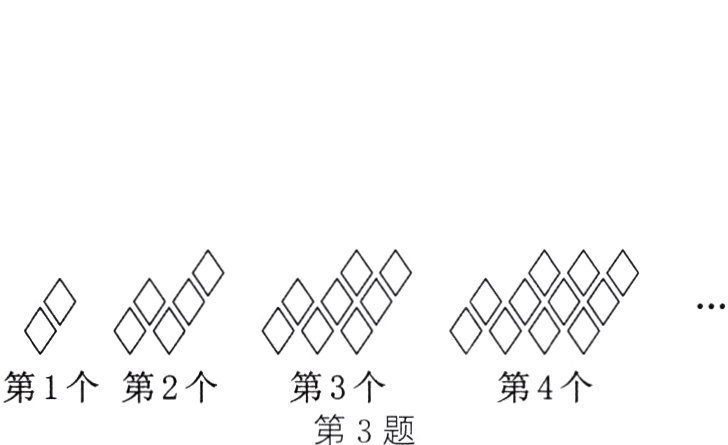
3.（2024·重庆B卷改编）用菱形按如图所示的规律拼图案，其中第1个图案中有2个菱形，第2个图案中有5个菱形，第3个图案中有8个菱形，第4个图案中有11个菱形……按此规律，设第x个图案中有y个菱形，则y与x之间的函数表达式为________.
　　　　　

答案： $y = 3x - 1$

4. 某市某工艺品厂生产一款工艺品，已知这款工艺品的生产成本为60元/件.现对该款工艺品每天的销售量与售价进行调查，整理如下表：
　
（1）以该款工艺品每天的售价为横坐标，销售量为纵坐标，在平面直角坐标系内画出相应的点，并选用一条适当的直线近似地表示销售量与售价之间的关系；
（2）直接写出该款工艺品每天的销售量y（件）与售价x（元/件）之间的函数表达式；
（3）当售价定为多少时，才能使该工艺品厂每天获得的利润为40000元[利润=（售价－成本）×销售量]?

答案：

(1) 如图所示
(2) 该款工艺品每天的销售量$y$(件)与售价$x$(元/件)之间的函数表达式为$y = - 100x + 10000$
(3) 由题意，得$(x - 60)( - 100x + 10000)=40000$，即$x^{2}-160x + 6400 = 0$.$\therefore (x - 80)^{2}=0$，解得$x_{1}=x_{2}=80$.$\therefore$当售价定为80元/件时，才能使该工艺品厂每天获得的利润为40000元