《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

9. 已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$，则$\frac{x^{2}+xy}{yz}$的值为_______.

答案： $\frac{5}{6}$

10. （2023·丽水）小慧同学在学习九年级数学时，发现有的学习内容是一个逐步特殊化的过程，请在如图所示的横线上填写适当的数值，感受这种特殊化的学习过程.
$\boxed{\frac{a}{x}=\frac{y}{c}}\xrightarrow{当x = y = b时}\boxed{\frac{a}{b}=\frac{b}{c}}\xrightarrow{当\frac{a}{c}=____时}\boxed{\frac{a}{b}=\frac{b}{c}=\sqrt{2}}$

答案： 2 解析：$\because \frac{a}{b}=\frac{b}{c}=\sqrt{2}$，$\therefore a = \sqrt{2}b$，$b = \sqrt{2}c$，即$c = \frac{b}{\sqrt{2}}$。
$\therefore \frac{a}{c}=\sqrt{2}b\div\frac{b}{\sqrt{2}} = 2$。$\therefore$当$\frac{a}{c}=2$时，$\frac{a}{b}=\frac{b}{c}=\sqrt{2}$。

11. 若△ABC的三边长a、b、c满足$a：b：c = 6：4：3$，设长为a、b、c的这三边上的高分别为$h_1$、$h_2$、$h_3$，则$h_1：h_2：h_3 =$_______.

答案： $2:3:4$ 解析：设$a = 6k(k\neq0)$，则$b = 4k$，$c = 3k$。根据三角形的面积公式，得$\frac{1}{2}ah_1=\frac{1}{2}bh_2=\frac{1}{2}ch_3$。化简，得$6h_1 = 4h_2 = 3h_3$，即$\frac{h_1}{2}=\frac{h_2}{3}=\frac{h_3}{4}$，$\therefore h_1:h_2:h_3 = 2:3:4$。

12. 已知$x：y = 3：5$，$3y = 2z$，求$\frac{x + y+z}{2x - y+z}$的值.

答案： $\because 3y = 2z$，$\therefore y:z = 2:3 = 10:15$。$\because x:y = 3:5 = 6:10$，$\therefore x:y:z = 6:10:15$。设$x = 6k(k\neq0)$，则$y = 10k$，$z = 15k$。$\therefore \frac{x + y+z}{2x - y + z}=\frac{6k + 10k + 15k}{12k - 10k + 15k}=\frac{31k}{17k}=\frac{31}{17}$

13. 已知有三条长度分别为2 cm、4 cm、8 cm的线段，请再添加一条线段，使这四条线段成比例. 求所添加线段的长度（写出所有结果）.

答案： 设所添加线段的长度为$a\text{ cm}$。①当$0 ＜ a ＜ 2$时，$8a = 2\times4$，解得$a = 1$；②当$2\leqslant a ＜ 8$时，$4a = 2\times8$，解得$a = 4$；③当$a\geqslant8$时，$2a = 4\times8$，解得$a = 16$。综上所述，所添加线段的长度为$1\text{ cm}$或$4\text{ cm}$或$16\text{ cm}$

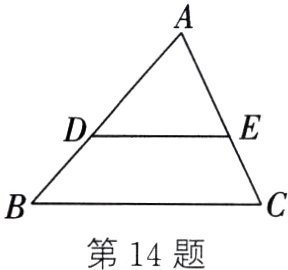
14. 如图，在△ABC中，$\frac{AD}{DB}=\frac{AE}{EC}$，$AB = 12$，$AE = 6$，$EC = 4$.
（1）求AD的长；
（2）求证：$\frac{DB}{AB}=\frac{EC}{AC}$.

答案：
(1)$\because AE = 6$，$EC = 4$，$\therefore \frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$。设$AD = 3k(k ＞ 0)$，则$DB = 2k$。$\therefore AB = AD + DB = 5k = 12$。$\therefore k = 2.4$。$\therefore AD = 3k = 7.2$
(2)由
(1)，知$AD = 7.2$。$\therefore DB = AB - AD = 12 - 7.2 = 4.8$。$\because AE = 6$，$EC = 4$，$\therefore AC = AE + EC = 6 + 4 = 10$。
$\therefore \frac{DB}{AB}=\frac{4.8}{12}=\frac{2}{5}$，$\frac{EC}{AC}=\frac{4}{10}=\frac{2}{5}$。$\therefore \frac{DB}{AB}=\frac{EC}{AC}$