第95页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
6. (2024·雅安)在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在点A处仰望楼顶,测得仰角为30°,再往楼房的方向前进50 m至点B处,测得仰角为60°,那么这栋楼房的高度为(人的身高忽略不计) ( )
A. 25√3 m B. 25 m C. 25√2 m D. 50 m
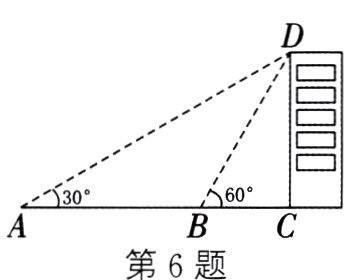
A. 25√3 m B. 25 m C. 25√2 m D. 50 m

答案:
A
7. (2024·赤峰)综合实践课上,航模小组用无人机测量古树AB的高度. 如图,点C处与古树底部A处在同一水平面上,且AC=10 m,无人机从点C处竖直上升到达点D处,测得古树顶部B的俯角为45°,古树底部A的俯角为65°,则古树AB的高度约为________m(精确到0.1 m,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.145).
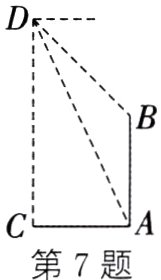

答案:
11.5
8. (2023·营口)为了丰富学生的文化生活,学校利用假期组织学生到A地和B地参观学习. 如图,学生从学校出发,走到C地时,发现A地位于C地的北偏西25°方向上,B地位于C地的北偏西55°方向上,老师将学生分成甲、乙两组,甲组前往A地,乙组前往B地,已知B地在A地的南偏西20°方向上,且相距1 000米,请求出甲组学生比乙组学生大约多走多远的路程(参考数据:√2≈1.41,√6≈2.45).
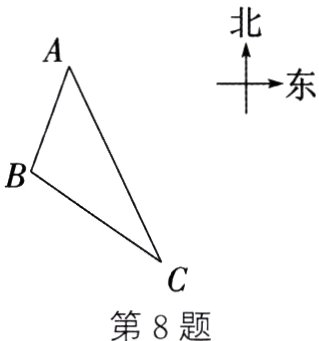

答案:
如图,过点B作BE⊥AC,垂足为E. 由题意,得∠ACD = 25°,∠BCD = 55°,∠FAB = 20°,AB = 1000米,CD//FA,
∴∠CAF = ∠ACD = 25°.
∴∠BAC = ∠FAB + ∠CAF = 45°,∠ACB = ∠BCD - ∠ACD = 30°.
∴在Rt△ABE中,AE = AB·cos 45° = 1000×$\frac{\sqrt{2}}{2}$ = 500√2(米),BE = AB·sin 45° = 1000×$\frac{\sqrt{2}}{2}$ = 500√2(米).
∴在Rt△BCE中,BC = $\frac{BE}{sin 30°}$ = 1000√2米,CE = $\frac{BE}{tan 30°}$ = 500√2÷$\frac{\sqrt{3}}{3}$ = 500√6(米).
∴AC = AE + CE = (500√2 + 500√6)米.
∴AC - BC = 500√2 + 500√6 - 1000√2 = 500√6 - 500√2 ≈ 520(米).
∴甲组学生比乙组学生大约多走520米的路程

如图,过点B作BE⊥AC,垂足为E. 由题意,得∠ACD = 25°,∠BCD = 55°,∠FAB = 20°,AB = 1000米,CD//FA,
∴∠CAF = ∠ACD = 25°.
∴∠BAC = ∠FAB + ∠CAF = 45°,∠ACB = ∠BCD - ∠ACD = 30°.
∴在Rt△ABE中,AE = AB·cos 45° = 1000×$\frac{\sqrt{2}}{2}$ = 500√2(米),BE = AB·sin 45° = 1000×$\frac{\sqrt{2}}{2}$ = 500√2(米).
∴在Rt△BCE中,BC = $\frac{BE}{sin 30°}$ = 1000√2米,CE = $\frac{BE}{tan 30°}$ = 500√2÷$\frac{\sqrt{3}}{3}$ = 500√6(米).
∴AC = AE + CE = (500√2 + 500√6)米.
∴AC - BC = 500√2 + 500√6 - 1000√2 = 500√6 - 500√2 ≈ 520(米).
∴甲组学生比乙组学生大约多走520米的路程

9. (2024·巴中)某兴趣小组开展了测量电线塔高度的实践活动. 如图,斜坡BE的坡度i=1∶√3,BE=6 m,在点B处测得电线塔CD顶部D的仰角为45°,在点E处测得电线塔CD顶部D的仰角为60°. 求:
(1)点B离水平地面的高度AB;
(2)电线塔CD的高度(结果保留根号).
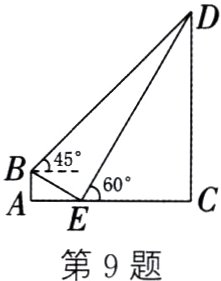
(1)点B离水平地面的高度AB;
(2)电线塔CD的高度(结果保留根号).

答案:
(1)由题意,得BA⊥AE.
∵斜坡BE的坡度i = 1 : √3,
∴在Rt△ABE中,tan∠BEA = $\frac{AB}{AE}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$.
∴∠BEA = 30°.
∵BE = 6 m,
∴易得AB = $\frac{1}{2}$BE = 3 m.
∴点B离水平地面的高度AB为3 m (2)如图,过点B作BF⊥CD,垂足为F,则四边形BACF为矩形.
∴AB = CF = 3 m,BF = AC. 设EC = x m.
∵在Rt△ABE中,AE = BE·cos 30° = 3√3 m,
∴BF = AC = AE + CE = (x + 3√3)m.
∵在Rt△CDE中,∠DEC = 60°,
∴CD = CE·tan 60° = √3x m.
∵在Rt△BDF中,∠DBF = 45°,
∴DF = BF·tan 45° = (x + 3√3)m.
∵DF + CF = CD,
∴x + 3√3 + 3 = √3x,解得x = 6 + 3√3.
∴CD = (6√3 + 9)m.
∴电线塔CD的高度为(6√3 + 9)m

(1)由题意,得BA⊥AE.
∵斜坡BE的坡度i = 1 : √3,
∴在Rt△ABE中,tan∠BEA = $\frac{AB}{AE}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$.
∴∠BEA = 30°.
∵BE = 6 m,
∴易得AB = $\frac{1}{2}$BE = 3 m.
∴点B离水平地面的高度AB为3 m (2)如图,过点B作BF⊥CD,垂足为F,则四边形BACF为矩形.
∴AB = CF = 3 m,BF = AC. 设EC = x m.
∵在Rt△ABE中,AE = BE·cos 30° = 3√3 m,
∴BF = AC = AE + CE = (x + 3√3)m.
∵在Rt△CDE中,∠DEC = 60°,
∴CD = CE·tan 60° = √3x m.
∵在Rt△BDF中,∠DBF = 45°,
∴DF = BF·tan 45° = (x + 3√3)m.
∵DF + CF = CD,
∴x + 3√3 + 3 = √3x,解得x = 6 + 3√3.
∴CD = (6√3 + 9)m.
∴电线塔CD的高度为(6√3 + 9)m

查看更多完整答案,请扫码查看


