《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

7. 一个三角形三边的长之比为3∶5∶7，与它相似的三角形的最长边的长是21 cm，则其余两边的长之和是（ ）
A. 15 cm
B. 18 cm
C. 21 cm
D. 24 cm

答案： D

8.（2023·威海）四边形ABCD是一张矩形纸片，将其按如图所示的方式折叠，使边AD落在边DC上，点A落在点H处，折痕为DE；使边BC落在边CD上，点B落在点G处，折痕为CF. 若矩形HEFG与原矩形ABCD相似，且AD = 1，则CD的长为_______.

答案： $\sqrt{2}+1$ 解析：设$HG = x$。$\because$四边形$ABCD$是矩形，$\therefore \angle A=\angle ADH = 90^{\circ}$，$AD = BC = 1$。由折叠，知$\angle DHE=\angle A = 90^{\circ}$，$AD = DH = 1$。$\therefore$四边形$ADHE$是矩形。$\therefore AD = HE = 1$。同理，可得$CG = 1$，$FG = 1$。$\because$矩形$HEFG$与原矩形$ABCD$相似，$\therefore \frac{HG}{AD}=\frac{FG}{CD}$。$\therefore \frac{x}{1}=\frac{1}{1 + x + 1}$，解得$x = \sqrt{2}-1$（负值舍去）。$\therefore CD = 1 + x + 1=\sqrt{2}+1$

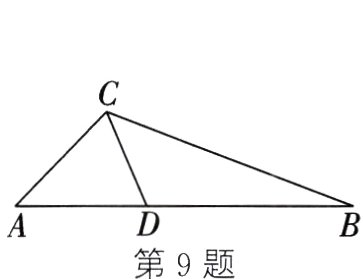
9. 经过三边都不相等的三角形的一个顶点的线段把这个三角形分成两个小三角形，如果其中一个小三角形是等腰三角形，另外一个小三角形和原三角形相似，那么把这条线段定义为原三角形的"和谐分割线". 如图，线段CD是△ABC的"和谐分割线"，△ACD为等腰三角形，△CBD∽△ABC，∠A = 46°，则∠ACB的度数为__________.

答案： $113^{\circ}$或$92^{\circ}$ 解析：由$\triangle CBD\backsim\triangle ABC$，得$\angle BCD=\angle A = 46^{\circ}$。$\because \triangle ACD$是等腰三角形，且$\angle ADC＞\angle BCD$，$\therefore \angle ADC＞\angle A$，即$AC\neq CD$。①当$AC = AD$时，$\angle ACD=\angle ADC=\frac{1}{2}\times(180^{\circ}-46^{\circ}) = 67^{\circ}$，此时$\angle ACB = 67^{\circ}+46^{\circ}=113^{\circ}$；②当$AD = CD$时，$\angle A=\angle ACD = 46^{\circ}$，此时$\angle ACB = 46^{\circ}+46^{\circ}=92^{\circ}$。

10. 如图，在□ABCD中，AC与BD交于点O，F、E、M、N分别是AO、BO、CO、DO的中点，连接FE、EM、MN、NF，得到□FEMN. 求证：□ABCD∽□FEMN.

答案： $\because F$、$E$分别是$AO$、$BO$的中点，$\therefore FE=\frac{1}{2}AB$，$FE// AB$。$\therefore \angle OEF=\angle OBA$，$\angle OFE=\angle OAB$。同理，可得$EM=\frac{1}{2}BC$，$MN=\frac{1}{2}CD$，$NF=\frac{1}{2}DA$，$\angle OEM=\angle OBC$，$\angle OME=\angle OCB$，$\angle OMN=\angle OCD$，$\angle ONM=\angle ODC$，$\angle ONF=\angle ODA$，$\angle OFN=\angle OAD$。$\therefore \frac{AB}{FE}=\frac{BC}{EM}=\frac{CD}{MN}=\frac{DA}{NF}$，易得$\angle DAB=\angle NFE$，$\angle ABC=\angle FEM$，$\angle BCD=\angle EMN$，$\angle CDA=\angle MNF$。$\therefore \square ABCD\backsim\square FEMN$

11. 如图，E是菱形ABCD的对角线CA的延长线上的任意一点，以线段AE为边，向下作菱形AEFG，且菱形AEFG∽菱形ABCD，连接EB、GD.
（1）求证：EB = GD；
（2）若∠DAB = 60°，AB = 2，AG = $\sqrt{3}$，求GD的长.

答案： （1）$\because$菱形$AEFG\backsim$菱形$ABCD$，$\therefore \angle EAG=\angle BAD$。$\therefore \angle EAG+\angle GAB=\angle BAD+\angle GAB$，即$\angle EAB=\angle GAD$。$\because$在菱形$AEFG$和菱形$ABCD$中，$AE = AG$，$AB = AD$，$\therefore \triangle AEB\cong\triangle AGD$。$\therefore EB = GD$ （2）连接$BD$，交$AC$于点$P$。$\because$四边形$ABCD$是菱形，$\therefore AD = AB = 2$，$BP\perp AC$，$BP=\frac{1}{2}BD$。$\because \angle DAB = 60^{\circ}$，$\therefore \triangle ABD$是等边三角形。$\therefore BD = 2$。$\therefore BP = 1$。$\therefore$在$Rt\triangle ABP$中，由勾股定理，得$AP=\sqrt{AB^{2}-BP^{2}}=\sqrt{3}$。$\because AE = AG=\sqrt{3}$，$\therefore EP = 2\sqrt{3}$。$\therefore$在$Rt\triangle EBP$中，由勾股定理，得$EB=\sqrt{EP^{2}+BP^{2}}=\sqrt{13}$。$\therefore GD = EB=\sqrt{13}$