《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

1. 如图，在平面直角坐标系内有一点P(3,4)，连接OP，则OP与x轴正方向所夹锐角α的正弦值是 （ ）

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$

答案： D

2. 如图，一辆小车沿倾斜角为α的斜坡向上行驶13 m. 若$\cos\alpha=\frac{12}{13}$，则小车上升的高度是 （ ）

A. 5 m
B. 6 m
C. 6.5 m
D. 12 m

答案： A

3. 在Rt△ABC中，∠C=90°，AC=1，BC=$\sqrt{2}$，则$\cos A$的值为_______.

答案： $\frac{\sqrt{3}}{3}$

4. 用计算器计算：$\sin35^{\circ}\approx$_______，$\cos35^{\circ}44'27''\approx$_______（精确到0.01）.

答案： 0.57 0.81

5. 如图，关于α与β的同一种三角函数值，有下列三个结论：①$\tan\alpha＞\tan\beta$；②$\sin\alpha＞\sin\beta$；③$\cos\alpha＞\cos\beta$. 其中，正确的是_______（填序号）.

答案： ①②

6. 如图，在正方形ABCD中，M是AD的中点，BE=3AE. 求∠ECM的正切值、正弦值及余弦值.

答案： 设正方形 $ABCD$ 的边长为 $4a$. $\because BE = 3AE$，$\therefore AE = a$，$BE = 3a$. $\because$ 四边形 $ABCD$ 是正方形，$\therefore \angle A=\angle B=\angle D = 90^{\circ}$. 在 $Rt\triangle BCE$ 中，$BE = 3a$，$BC = 4a$，$\therefore$ 由勾股定理，得 $EC=\sqrt{BE^{2}+BC^{2}} = 5a$. $\because M$ 是 $AD$ 的中点，$\therefore AM = MD=\frac{1}{2}AD = 2a$. $\therefore$ 在 $Rt\triangle AEM$ 中，由勾股定理，得 $EM=\sqrt{AE^{2}+AM^{2}}=\sqrt{5}a$，在 $Rt\triangle CDM$ 中，由勾股定理，得 $MC=\sqrt{MD^{2}+CD^{2}} = 2\sqrt{5}a$. $\therefore EM^{2}+MC^{2}=EC^{2}$. $\therefore \angle EMC = 90^{\circ}$. $\therefore$ 在 $Rt\triangle CEM$ 中，$\tan\angle ECM=\frac{EM}{MC}=\frac{1}{2}$，$\sin\angle ECM=\frac{EM}{EC}=\frac{\sqrt{5}}{5}$，$\cos\angle ECM=\frac{MC}{EC}=\frac{2\sqrt{5}}{5}$

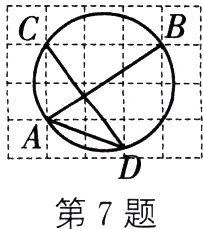
7. 如图，在由边长为1的小正方形构成的网格中，点A、B、C都在格点上，以AB为直径的圆经过点C、D，则$\cos\angle ADC$的值为 （ ）

A. $\frac{2\sqrt{13}}{13}$
B. $\frac{3\sqrt{13}}{13}$
C. $\frac{2}{3}$
D. $\frac{\sqrt{5}}{5}$

答案： B