《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

1. 已知P为线段AB的黄金分割点，且AP＜PB，则下列结论正确的是 （ ）
A. AP²=AB·PB
B. AB²=AP·PB
C. PB²=AP·AB
D. AP²+BP²=AB²

答案： C

2. 矩形的两条相邻的边的长分别为a、b，下列数据能构成黄金矩形（宽与长的比为黄金比的矩形）的是 （ ）
A. a=4，b=√5+2
B. a=4，b=√5 - 2
C. a=4，b=2√5+4
D. a=4，b=2√5 - 2

答案： D

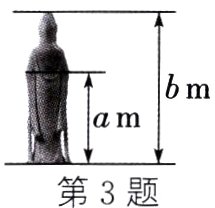
3. 生活中到处可见黄金分割的美. 如图，在设计人体雕像时，使雕像腰部以下的高度a与全身的高度b的比值接近0.618，可以增加视觉美感. 若图中b的值为2，则a的值约为 （ ）
A. 1.24 B. 1.38 C. 1.42 D. 1.62
　　　　　　　

答案： A

4. 如图，若B是线段AC的黄金分割点(AB＞BC)，AC=20 cm，则AB的长为_______cm.
　　　　　　

答案： (10$\sqrt{5}$ - 10)

5. 电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体. 如图，若舞台AB的长为20 m，则主持人应走到离点A至少_______m处最合适(精确到0.1 m).
　　　　　　

答案： 7.6 解析：舞台 $AB$ 上有两个黄金分割点，由于题中涉及“至少”，则所求距离为 $20\times(1 - \frac{\sqrt{5}-1}{2})\approx7.6(m)$。$\therefore$ 主持人应走到离点 $A$ 至少 $7.6m$ 处最合适。

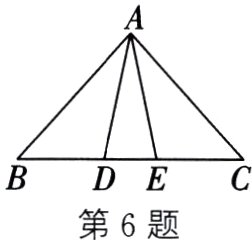
6. 如图，在△ABC中，AB=AC=3，BC=4. 若D、E是边BC的两个黄金分割点，求△ADE的面积.
　

答案： 过点 $A$ 作 $AH\perp BC$ 于点 $H$。$\because AB = AC$，$AH\perp BC$，$\therefore BH = CH=\frac{1}{2}BC = 2$。$\therefore$ 在 $Rt\triangle AHB$ 中，由勾股定理，得 $AH = \sqrt{3^{2}-2^{2}}=\sqrt{5}$。$\because D$、$E$ 是边 $BC$ 的两个黄金分割点，$\therefore$ 易得 $BE=\frac{\sqrt{5}-1}{2}BC = 2\sqrt{5}-2$。$\therefore HE = BE - BH = 2\sqrt{5}-2 - 2 = 2\sqrt{5}-4$。同理，可得 $DH = 2\sqrt{5}-4$。$\therefore DE = HE + DH = 4\sqrt{5}-8$。$\therefore S_{\triangle ADE}=\frac{1}{2}DE\cdot AH=\frac{1}{2}\times(4\sqrt{5}-8)\times\sqrt{5}=10 - 4\sqrt{5}$

7. （2024·德阳）宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形称为黄金矩形，黄金矩形给我们以协调的美感，世界各国许多著名建筑为取得最佳的视觉效果，都采用了黄金矩形的设计. 已知四边形ABCD是黄金矩形(AB＜BC)，P是边AD上一点，则满足PB⊥PC的点P的个数为 （ ）
A. 3
B. 2
C. 1
D. 0

答案：
D 解析：如图。$\because PB\perp PC$，$\therefore$ 点 $P$ 在以 $BC$ 为直径的 $\odot M$ 上。根据四边形 $ABCD$ 是黄金矩形，不妨设 $AB = CD = (\sqrt{5}-1)a$，$AD = BC = 2a$，此时 $\odot M$ 的半径为 $a$。$\because (\sqrt{5}-1)a\approx1.236a ＞ a$，$\therefore$ 边 $AD$ 与 $\odot M$ 相离。$\therefore$ 边 $AD$ 上不存在满足 $PB\perp PC$ 的点 $P$，即满足 $PB\perp PC$ 的点 $P$ 的个数为 $0$。