《2025年通城学典课时作业本九年级数学下册苏科版江苏专版》

15. （2024·资阳）如图，某海域有两灯塔A、B，其中灯塔B在灯塔A的南偏东30°方向，且灯塔A、B相距$\frac{16\sqrt{3}}{3}$海里. 一渔船在C处捕鱼，测得C处在灯塔A的北偏东30°方向，在灯塔B的正北方向.
（1）求B、C两处的距离.
（2）该渔船从C处沿北偏东65°方向航行一段时间后，突发故障滞留于D处，并发出求救信号. 此时，在灯塔B处的渔政船测得D处在北偏东27°方向，便立即以18海里/时的速度沿BD方向航行至D处救援，求渔政船的航行时间（注：点A、B、C、D在同一水平面内，参考数据：tan65°≈2.1，tan27°≈0.5）.
　　　　

答案：

(1) 如图，由题意，得$BC// EF$，$\therefore\angle ACB=\angle CAE = 30^{\circ}$，$\angle ABC=\angle BAF = 30^{\circ}$。$\therefore\angle ACB=\angle ABC$。$\therefore AB = AC=\frac{16\sqrt{3}}{3}$海里。过点$A$作$AH\perp BC$于点$H$。$\therefore\angle AHC=\angle AHB = 90^{\circ}$，$CH = BH$。$\therefore CH = BH = AB\cdot\cos30^{\circ}=\frac{16\sqrt{3}}{3}\times\frac{\sqrt{3}}{2}=8$(海里)。$\therefore BC = CH + BH = 16$海里。$\therefore B$、$C$两处的距离为16海里
(2) 如图，过点$D$作$DG\perp BC$，交$BC$的延长线于点$G$。设$DG = x$海里。在$Rt\triangle BDG$中，$BG=\frac{DG}{\tan27^{\circ}}\approx2x$海里，在$Rt\triangle CDG$中，$CG=\frac{DG}{\tan65^{\circ}}\approx\frac{x}{2.1}$海里。$\because BC = BG - CG$，$\therefore 2x-\frac{x}{2.1}=16$，解得$x = 10.5$。$\therefore DG = 10.5$海里。$\therefore CG = 5$海里，$BG = 21$海里。$\therefore BD=\sqrt{BG^{2}+DG^{2}}=\frac{21\sqrt{5}}{2}$海里。$\therefore$渔政船的航行时间为$\frac{21\sqrt{5}}{2}\div18=\frac{7\sqrt{5}}{12}$(小时)

16. 如图，在Rt△ABC中，∠ACB = 90°，CE是斜边AB上的中线，过点E作EF⊥AB，交AC于点F. 若BC = 4，△AEF的面积为5，则sin∠CEF的值为 （ ）
A. $\frac{3}{5}$ B. $\frac{\sqrt{5}}{5}$ C. $\frac{4}{5}$ D. $\frac{2\sqrt{5}}{5}$
　　　　　　　

答案： A

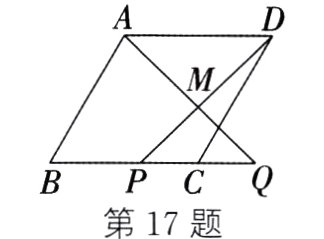
17. （2024·乐山）如图，在菱形ABCD中，∠ABC = 60°，AB = 1，P是边BC上一个动点，在BC的延长线上找一点Q，使得点P和点Q关于点C对称，连接DP、AQ交于点M. 当点P从点B运动到点C时，点M的运动轨迹的长为_______.
　　　

答案：
$\frac{\sqrt{3}}{3}$ 解析：如图，连接$AC$，过点$C$作$CG\perp BC$，交$AD$于点$G$，作点$B$关于点$C$的对称点$Q'$，连接$BD$、$AQ'$交于点$H$。$\because$四边形$ABCD$是菱形，$\angle ABC = 60^{\circ}$，$\therefore AD// BC$，$AD = CD = AB = BC$，$\angle ADC=\angle ABC = 60^{\circ}$，$\angle DBC=\frac{1}{2}\angle ABC = 30^{\circ}$。$\therefore\triangle ACD$是等边三角形，$CG\perp AD$。$\therefore CG$垂直平分$AD$。$\because$点$P$、$Q$关于点$C$对称，$\therefore$易得点$M$一定在直线$CG$上。$\because$点$P$从点$B$运动到点$C$，$\therefore$可以得到点$M$的运动轨迹就是$CH$这一段。$\because$在$Rt\triangle BCH$中，$\angle DBC = 30^{\circ}$，$BC = AB = 1$，$\therefore CH = BC\times\tan30^{\circ}=\frac{\sqrt{3}}{3}$，即点$M$的运动轨迹的长为$\frac{\sqrt{3}}{3}$。

18. 如图，在Rt△ABC中，∠ACB = 90°，∠B = 60°，BC = 2，P为斜边AB上的一个动点（点P不与点A、B重合），过点P作PD⊥AC，PE⊥BC，垂足分别为D、E，连接DE、PC交于点Q，连接AQ. 当△APQ为直角三角形时，AP的长为_______.
　　　　

答案： 3或$2\sqrt{3}$

19. （2024·广安改编）如图，∠AOB的边OB与x轴的正半轴重合，P是OA上一动点，N（3，0）是OB上一定点，M是ON的中点，∠AOB = 30°，要使PM + PN的值最小，则点P的坐标为_______.
　　　　　　　　　　　　

答案： $(\frac{3}{2},\frac{\sqrt{3}}{2})$ 解析：作点$N$关于$OA$对称的点$N'$，连接$N'M$，交$OA$于点$P$，此时$PM + PN$的值最小，连接$ON'$。根据题意，可证$\triangle NON'$是等边三角形，结合$M$是$ON$的中点，可得$N'M\perp ON$。在$Rt\triangle PMO$中，$OM=\frac{1}{2}ON=\frac{3}{2}$，$PM = OM\cdot\tan30^{\circ}=\frac{\sqrt{3}}{2}$，$\therefore$点$P$的坐标为$(\frac{3}{2},\frac{\sqrt{3}}{2})$。

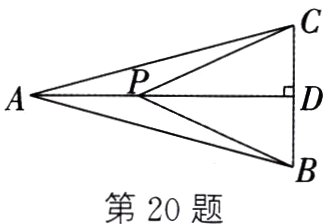
20. 如图，在△ABC中，AB = AC = 4，∠CAB = 30°，AD⊥BC，垂足为D，P为线段AD上的一动点，连接PB、PC，则PA + 2PB的最小值为_______.
　　　　　　　

答案：
$4\sqrt{2}$ 解析：如图，在$\angle BAC$的外部作$\angle CAE = 15^{\circ}$，过点$B$作$BF\perp AE$于点$F$，交$AD$于点$P$，此时$PA + 2PB$的值最小。$\therefore\angle AFB = 90^{\circ}$。$\because AB = AC$，$AD\perp BC$，$\therefore\angle CAD=\angle BAD=\frac{1}{2}\angle BAC=\frac{1}{2}\times30^{\circ}=15^{\circ}$。$\therefore\angle EAD=\angle CAE+\angle CAD = 30^{\circ}$。$\therefore PF=\frac{1}{2}PA$。$\therefore PA + 2PB = 2(\frac{1}{2}PA + PB)=2(PF + PB)=2BF$。在$Rt\triangle ABF$中，$AB = 4$，$\angle BAF=\angle BAC+\angle CAE = 45^{\circ}$，$\therefore BF = AB\cdot\sin45^{\circ}=4\times\frac{\sqrt{2}}{2}=2\sqrt{2}$。$\therefore PA + 2PB$的最小值$=2BF = 4\sqrt{2}$。