第102页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 甲、乙、丙3名射击运动员在某场测试中各射击20次,3人的测试成绩如下表:
|项目|甲|乙|丙|

|成绩/环|7 8 9 10|7 8 9 10|7 8 9 10|
|频数|4 6 6 4|6 4 4 6|5 5 5 5|
通过计算,判断甲、乙、丙3名运动员谁的测试成绩最稳定.
|项目|甲|乙|丙|

|成绩/环|7 8 9 10|7 8 9 10|7 8 9 10|
|频数|4 6 6 4|6 4 4 6|5 5 5 5|
通过计算,判断甲、乙、丙3名运动员谁的测试成绩最稳定.
答案:
解:$\overline{x}_$甲$=\frac {7×4+8×6+9×6+10×4}{20}=8.5($环)
$\overline{x}_$乙$=\frac {7×6+8×4+9×4+10×6}{20}=8.5($环)
$\overline{x}_$丙$=\frac {7×5+8×5+9×5+10×5}{20}=8.5($环)
$s^2_$甲$=\frac 1{20}×[4×(7-8.5)^2+6×(8-8.5)^2+6×(9-8.5)^2+4×(10-8.5)^2]=1.05($环$^2)$
$s^2_$乙$=\frac 1{20}×[6×(7-8.5)^2+4×(8-8.5)^2+4×(9-8.5)^2+6×(10-8.5)^2]=1.45($环$^2)$
$s^2_$丙$=\frac 1{20}×[5×(7-8.5)^2+5×(8-8.5)^2+5×(9-8.5)^2+5×(10-8.5)^2]=1.25($环$^2)$
$s^2_$乙$\gt s^2_$丙$\gt s^2_$甲
∴甲的测试成绩最稳定.
$\overline{x}_$乙$=\frac {7×6+8×4+9×4+10×6}{20}=8.5($环)
$\overline{x}_$丙$=\frac {7×5+8×5+9×5+10×5}{20}=8.5($环)
$s^2_$甲$=\frac 1{20}×[4×(7-8.5)^2+6×(8-8.5)^2+6×(9-8.5)^2+4×(10-8.5)^2]=1.05($环$^2)$
$s^2_$乙$=\frac 1{20}×[6×(7-8.5)^2+4×(8-8.5)^2+4×(9-8.5)^2+6×(10-8.5)^2]=1.45($环$^2)$
$s^2_$丙$=\frac 1{20}×[5×(7-8.5)^2+5×(8-8.5)^2+5×(9-8.5)^2+5×(10-8.5)^2]=1.25($环$^2)$
$s^2_$乙$\gt s^2_$丙$\gt s^2_$甲
∴甲的测试成绩最稳定.
2. 一家公司从某大学的应届毕业生中招聘职员,对应聘者的专业知识、英语水平、社会实践经验等3项进行测试或成果认定,3项的满分都为100分,3项的分数分别按5∶3∶2的比例记入每人的最后总分,4位应聘者的得分如下表(单位:分):
|应聘者|得分| | |
| |专业知识|英语水平|社会实践经验|
|A|85|85|90|
|B|85|85|70|
|C|80|90|70|
|D|90|90|50|
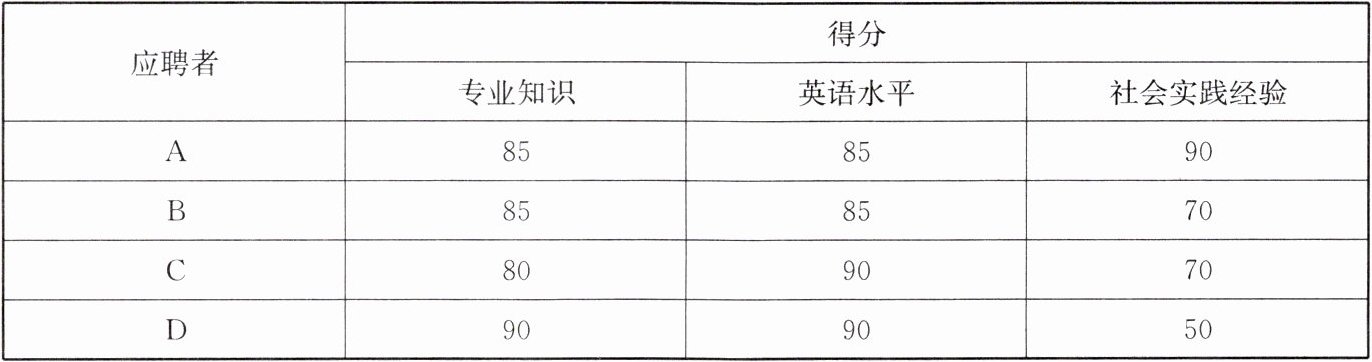
(1) 写出4位应聘者的总分;
(2) 分别对专业知识、英语水平、社会实践经验3项得分的数据,求4人的方差.
(3) 由(1)和(2),你对应聘者有何建议?
|应聘者|得分| | |
| |专业知识|英语水平|社会实践经验|
|A|85|85|90|
|B|85|85|70|
|C|80|90|70|
|D|90|90|50|

(1) 写出4位应聘者的总分;
(2) 分别对专业知识、英语水平、社会实践经验3项得分的数据,求4人的方差.
(3) 由(1)和(2),你对应聘者有何建议?
答案:
解:$( 1 )\ \mathrm {A}$:85×50\%+85×30\%+90×20\%=86( 分 )
B:85×50\%+85×30\%+70×20\%=82( 分 )
C:80×50\%+90×30\%+70×20\%=81( 分 )
D:90×50\%+90×30\%+50×20\%=82( 分 )
( 2 ) 专业知识得分的平均数:$\bar{x}_1=\frac {85+85+80+90}{4}=85( $分 )
方差:$s_1^2=\frac {(85-85)^2+( 85-85 ) ^2+( 80-85 ) ^2+( 90-85 ) ^2}{4}=12.5( $分$^2 )$
英语水平得分的平均数:$\bar{x}_2=\frac {85+85+90+90}{4}=87.5( $分 )
方差:$s_2^2=\frac {(85-87.5)^2+( 85-87.5 ) ^2+( 90-87.5 ) ^2+( 90-87.5 ) ^2}{4}=6.25($分$^2)$
社会实践经验得分的平均数:$\bar{x}_3=\frac {90+90+70+50}{4}=70( $分 )
方差:$s_3^2=\frac {(90-70)^2+( 70-70 ) ^2+( 70-70 ) ^2+( 50-70 ) ^2}{4}=200( $分$^2 )$
( 3 ) 建议应聘者要多参加社会活动,提高社会实践经验.
解:$( 1 )\ \mathrm {A}$:85×50\%+85×30\%+90×20\%=86( 分 )
B:85×50\%+85×30\%+70×20\%=82( 分 )
C:80×50\%+90×30\%+70×20\%=81( 分 )
D:90×50\%+90×30\%+50×20\%=82( 分 )
( 2 ) 专业知识得分的平均数:$\bar{x}_1=\frac {85+85+80+90}{4}=85( $分 )
方差:$s_1^2=\frac {(85-85)^2+( 85-85 ) ^2+( 80-85 ) ^2+( 90-85 ) ^2}{4}=12.5( $分$^2 )$
英语水平得分的平均数:$\bar{x}_2=\frac {85+85+90+90}{4}=87.5( $分 )
方差:$s_2^2=\frac {(85-87.5)^2+( 85-87.5 ) ^2+( 90-87.5 ) ^2+( 90-87.5 ) ^2}{4}=6.25($分$^2)$
社会实践经验得分的平均数:$\bar{x}_3=\frac {90+90+70+50}{4}=70( $分 )
方差:$s_3^2=\frac {(90-70)^2+( 70-70 ) ^2+( 70-70 ) ^2+( 50-70 ) ^2}{4}=200( $分$^2 )$
( 3 ) 建议应聘者要多参加社会活动,提高社会实践经验.
查看更多完整答案,请扫码查看


