《2024年课课练九年级数学上册苏科版》

8. 第一组数据为 0,0,0,1,1,1,第二组数据为：$\underbrace{0,0,…,0}_{m个},\underbrace{1,1,…,1}_{n个}$,其中 m、n是正整数.有下列结论：
① 当$m= n$时,两组数据的平均数相等；
② 当$m＞n$时,第一组数据的平均数小于第二组数据的平均数；
③ 当$m＜n$时,第一组数据的中位数小于第二组数据的中位数；
④ 当$m= n$时,第二组数据的方差小于第一组数据的方差.
请通过计算,写出所有正确结论的序号.

答案： 解：①第 1 组平均数为： 0.5 .
当 m=n 时，
第 2 组平均数为:
$\frac {0 \times m+1 \times n}{m+n}=\frac {m}{2\ \mathrm {m}}=0.5\ $
$.\therefore ①$正确.
$\text { ②当 } m\gt n \text { 时, }\ $
$m+n\gt 2 n \text {, } \\\frac {n}{m+n}\lt 0.5 .$
$\therefore $第 1 组数据的平均数大于第 2 组数据的平均 数.
$\therefore ②$错误.
③第 1 组数据的中位数
$\ \frac {0+1}{2}=0.5$
当 m＜n时若m+ n为奇数，
第2组数据的中位数是1，
若m+ n为偶数，
第2组数据的中位数是1，
$\therefore $当$ m\lt n $时, 第 2 组数据的中位数是 1 ,
$\therefore m\lt n$时，
第1组数据的中位数小于第2组数据的
中位数.
$\therefore ③$正确.
④第1组数据的方差:
$\frac {3 \times(0-0.5)^2+3(1-0.5)^2}{6}=0.25 .$
第 2 组数据的方差:
$\frac {m(0-0.5)^2+n(1-0.5)^2}{m+n}=0.25\ $
$\therefore $当 m=n 时，
\ 第 2 组数据的方差等于第 1 组 数据的
方差.
$\therefore ④$错误.
所以正确结论的序号为①，③.

9. 某公司为提高服务质量,对某个部门开展了客户满意度问卷调查,客户满意度由低到高分为 1 分、2 分、3 分、4 分、5 分.公司规定：若客户所评分数的平均数或中位数低于 3.5 分,则该部门需要进行整改.工作人员从收回的问卷中随机抽取了20 份,并根据这 20 份问卷中的客户所评分数绘制成如下统计图.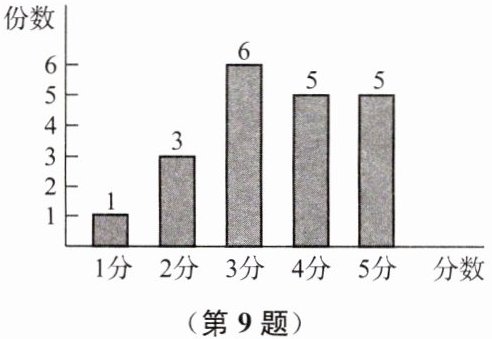
(1)求这 20 份问卷中的客户评分的平均数、中位数,并判断该部门是否需要整改.
(2)监督人员从余下的问卷中又随机抽取了 1 份,与之前的 20 份合在一起重新计算后,发现客户所评分数的平均数大于 3.55 分.监督人员抽取的问卷所评分数为几分？此时中位数是否发生变化？

答案： 解：$(1)\overline{x}=\frac {1+3×2+6×3+5×4+5×5}{20}=3.5($分)
中间两个数为3和4，$\frac {3+4}{2}=3.5($分)
不需要整改。
(2)3.55×21－3.5×20=4.55(分)
因此抽取的问卷所评的分数为5分
此时中位数是第11位人员的评分，为4分
因此中位数发生变化。