第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
10. 学校在八、九年级各抽取 50 名学生开展科普知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分 10 分.竞赛成绩的数据如图和表所示:
|年级|众数|中位数|方差|
|八年级|7|8|1.88|
|九年级|a|8|b|

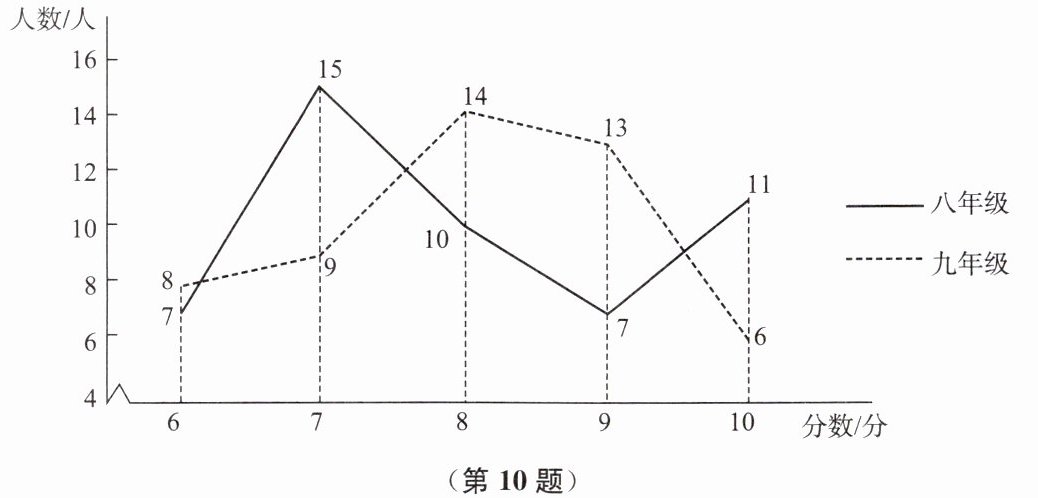
(1)你能用成绩的平均数判断哪个年级的成绩较好吗?通过计算说明.
(2)请根据图表中的信息,回答下列问题.
① 表中的$a= $______,$b= $______.
② 现要给成绩较好的年级颁最佳组织奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁最佳组织奖?
(3)若规定成绩为 10 分获一等奖,成绩为 9 分获二等奖,成绩为 8 分获三等奖,则哪个年级的获奖率高?
|年级|众数|中位数|方差|
|八年级|7|8|1.88|
|九年级|a|8|b|


(1)你能用成绩的平均数判断哪个年级的成绩较好吗?通过计算说明.
(2)请根据图表中的信息,回答下列问题.
① 表中的$a= $______,$b= $______.
② 现要给成绩较好的年级颁最佳组织奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁最佳组织奖?
(3)若规定成绩为 10 分获一等奖,成绩为 9 分获二等奖,成绩为 8 分获三等奖,则哪个年级的获奖率高?
答案:
8
1.56
解:
(1)不能,由题意,得八 年级竞赛成绩的平均数是
(6×7+7×15+8×10+9×7+10×11) ÷50= 8(分)
九年级竞赛成绩的平均数是
(6×8+7×9+8×14+9×13+10×6)÷50=8(分)
∴用竞赛成绩的平均数无法判断哪个年级的竞赛成绩比较好.
(2)②从众数和方差两个角度来看,应该给九年级颁最佳组织奖.
(3)八年级:(10+7+11)÷50=56\%
九年级:(14+13+6)÷50=66\%
因为66\%>56\%所以九年级获奖率高.
8
1.56
解:
(1)不能,由题意,得八 年级竞赛成绩的平均数是
(6×7+7×15+8×10+9×7+10×11) ÷50= 8(分)
九年级竞赛成绩的平均数是
(6×8+7×9+8×14+9×13+10×6)÷50=8(分)
∴用竞赛成绩的平均数无法判断哪个年级的竞赛成绩比较好.
(2)②从众数和方差两个角度来看,应该给九年级颁最佳组织奖.
(3)八年级:(10+7+11)÷50=56\%
九年级:(14+13+6)÷50=66\%
因为66\%>56\%所以九年级获奖率高.
查看更多完整答案,请扫码查看


