第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
8. 如图,圆锥底面的半径为10 cm,高为$10\sqrt{15}$ cm.
(1)求圆锥的全面积;
(2)一只蚂蚁从底面上一点A出发绕圆锥爬行一周回到SA上的点M处,已知SM= 3AM,求蚂蚁爬行的最短路程.

(1)求圆锥的全面积;
(2)一只蚂蚁从底面上一点A出发绕圆锥爬行一周回到SA上的点M处,已知SM= 3AM,求蚂蚁爬行的最短路程.

答案:
解:
(1)由题意,可得圆锥的母线$SA=\sqrt{AO^2+SO^2}=40(\ \mathrm {cm})$
圆锥的侧面展开扇形的弧长$l=2\pi \cdot OA=20\pi\ \mathrm {cm}$
$\therefore S_{侧}=\dfrac{1}{2}L\cdot SA=400\pi\ \mathrm {cm^2}$
$S_{圆}=\pi AO^2=100\pi\ \mathrm {cm^2},$
$\therefore S_{全}=S_{圆}+S_{底}=(400+100)\pi =500\pi (\ \mathrm {cm^2})$
解:
(2)沿母线SA将圆锥的侧面展
开,如图,
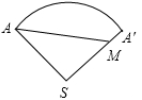
则线段AM的长就是蚂蚁所走的最短
距离
由
(1)知,
$SA=40\ \mathrm {cm},$
弧$AA'=20\pi\ \mathrm {cm}$
$\because \dfrac{n\pi \times 40}{180}=20\pi\ \mathrm {cm},$
$\therefore \angle S=n=\dfrac{180\times 20\pi }{40\pi }=90^{\circ},$
$\because SA'=SA=40\ \mathrm {cm},$SM=3A'M
$\therefore SM=30\ \mathrm {cm},$
$\therefore $在$Rt\triangle ASM$中,
由勾股定理得$AM=50(\ \mathrm {cm})$
所以,蚂蚁所走的最短距离是$50\ \mathrm {cm}. $
解:
(1)由题意,可得圆锥的母线$SA=\sqrt{AO^2+SO^2}=40(\ \mathrm {cm})$
圆锥的侧面展开扇形的弧长$l=2\pi \cdot OA=20\pi\ \mathrm {cm}$
$\therefore S_{侧}=\dfrac{1}{2}L\cdot SA=400\pi\ \mathrm {cm^2}$
$S_{圆}=\pi AO^2=100\pi\ \mathrm {cm^2},$
$\therefore S_{全}=S_{圆}+S_{底}=(400+100)\pi =500\pi (\ \mathrm {cm^2})$
解:
(2)沿母线SA将圆锥的侧面展
开,如图,

则线段AM的长就是蚂蚁所走的最短
距离
由
(1)知,
$SA=40\ \mathrm {cm},$
弧$AA'=20\pi\ \mathrm {cm}$
$\because \dfrac{n\pi \times 40}{180}=20\pi\ \mathrm {cm},$
$\therefore \angle S=n=\dfrac{180\times 20\pi }{40\pi }=90^{\circ},$
$\because SA'=SA=40\ \mathrm {cm},$SM=3A'M
$\therefore SM=30\ \mathrm {cm},$
$\therefore $在$Rt\triangle ASM$中,
由勾股定理得$AM=50(\ \mathrm {cm})$
所以,蚂蚁所走的最短距离是$50\ \mathrm {cm}. $
9. 工人师傅要把一块矩形铁皮加工成一个底面半径为20 cm、高为$40\sqrt{2}$ cm的圆锥形漏斗,要求只有一条接缝(接缝尺寸忽略不计).请你设计两种不同的裁剪方案画图并计算,比较哪种方案用料最少.此时所需矩形铁皮的长、宽分别为多少?
答案:
解:圆锥的母线长:
${\sqrt {{20}^{2}+{(40{\sqrt {2}})}^{2}}}=60(cm)$
设这个圆锥展开后的圆心角为n°
,则${\frac {nπ×60} {180}}=2π×20$
解得,n=120
方案一如图1,
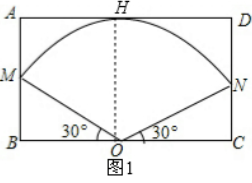
OM=OH=60cm,∠MON=120°
在Rt△OBM中,
∵ OM=60cm,∠MOB=30°
∴BM=30cm,
$OB={\sqrt {{OM}^{2}-{BM}^{2}}}=30{\sqrt {3}}cm$
∴$ BC=2OB=60\sqrt {3}cm$
∴ 方案一所需矩形铁皮的面积:
$60×60{\sqrt {3}}=3600{\sqrt {3}}(cm^2)$
方案二如图2,
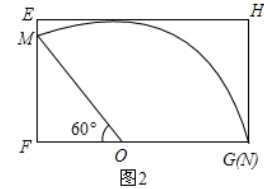
OM=EF=60cm,∠MON=120°
在Rt△MOF中,
∵ OM=60cm,∠MOF=60°
∴$ OF=\frac 1 2OM=30cm$
∴ FG=OF+OG=90cm
∴ 方案二所需矩形铁皮的面积:
$90×60=5400(cm^2)$
∵$ 5400<3600\sqrt {3}$
∴ 方案二用料最少,此时所需矩形铁
皮的长为90cm,宽为60cm.
解:圆锥的母线长:
${\sqrt {{20}^{2}+{(40{\sqrt {2}})}^{2}}}=60(cm)$
设这个圆锥展开后的圆心角为n°
,则${\frac {nπ×60} {180}}=2π×20$
解得,n=120
方案一如图1,

OM=OH=60cm,∠MON=120°
在Rt△OBM中,
∵ OM=60cm,∠MOB=30°
∴BM=30cm,
$OB={\sqrt {{OM}^{2}-{BM}^{2}}}=30{\sqrt {3}}cm$
∴$ BC=2OB=60\sqrt {3}cm$
∴ 方案一所需矩形铁皮的面积:
$60×60{\sqrt {3}}=3600{\sqrt {3}}(cm^2)$
方案二如图2,

OM=EF=60cm,∠MON=120°
在Rt△MOF中,
∵ OM=60cm,∠MOF=60°
∴$ OF=\frac 1 2OM=30cm$
∴ FG=OF+OG=90cm
∴ 方案二所需矩形铁皮的面积:
$90×60=5400(cm^2)$
∵$ 5400<3600\sqrt {3}$
∴ 方案二用料最少,此时所需矩形铁
皮的长为90cm,宽为60cm.
查看更多完整答案,请扫码查看


