《2025年新课程自主学习与测评九年级数学上册人教版》

21. (12 分)已知抛物线 $y = ax^{2}+bx + c$ 经过点 $(2,1)$,$(-1,-8)$,$(0,-3)$。
(1)求这个抛物线的解析式；
(2)画出该抛物线的草图；
(3)观察你所画出的抛物线的草图,写出 $x$ 在什么范围内取值时,函数值 $y＞0$。

答案： （1）抛物线的解析式$ y=-x^{2}+4x-3 $;（2）画图略;（3）$ 1＜x＜3 $

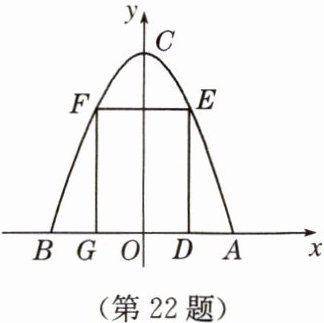
22. (10 分)如图,有一块高和宽都为 4 dm 的抛物线形的钢板,能从中截下一块周长为 8 dm 的长方形钢板吗？(提示：建立如图所示的平面直角坐标系)

答案： 提示:$ A(2,0) $,$ B(-2,0) $,$ C(0,4) $,则抛物线的解析式为$ y=-x^{2}+4 $.设点$ D(a,0) $,则点$ E(a,-a^{2}+4) $.所以长方形的周长为$ 2(2a-a^{2}+4) $.若$ 2(2a-a^{2}+4)=8 $,解得$ a=0 $或$ a=2 $(都不合题意,舍去).故不能截下一块周长为8 dm的长方形钢板.

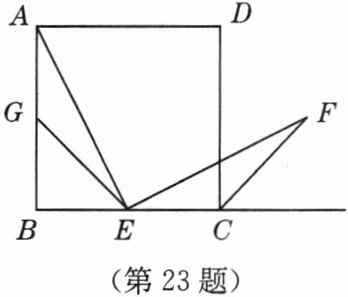
23. (10 分)如图,四边形 $ABCD$ 是正方形,点 $E$ 是边 $BC$ 的中点,且$\angle AEF = 90^{\circ}$,$EF$ 交正方形外角平分线 $CF$ 于点 $F$,取边 $AB$ 的中点 $G$,连接 $EG$。
(1)求证：$EG = CF$；
(2)将 $\triangle ECF$ 绕点 $E$ 逆时针旋转 $90^{\circ}$,请在图中直接画出旋转后的图形,并指出旋转后 $CF$ 与 $EG$ 的位置关系,并说明理由。

答案： （1）提示:证$ \angle ECF=\angle AGE=135^{\circ} $,$ \triangle AGE \cong \triangle ECF $;（2）$ CF // EG $,理由略.

24. (10 分)某商店进了一批皮鞋,进货价为 150 元/双,若按每双 200 元出售,则可销售 200 双。若每双皮鞋提价 5 元出售,则其销售量就减少 10 双。现在预计要获得 11200 元利润,应该每双鞋多少元出售？这时应进多少双皮鞋？

答案： 每双皮鞋按220元出售时,应进160双皮鞋;每双皮鞋按230元出售时,应进140双皮鞋.