第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
2. 用配方法解一元二次方程 $ 2x^{2}+4x - 5 = 0 $ 时,将它化为 $ (x + a)^{2}= b $ 的形式,则 $ a + b $ 的值为 ( )
A.$ 8 $
B.$ \dfrac{9}{2} $
C.$ \dfrac{7}{2} $
D.$ \dfrac{5}{2} $
A.$ 8 $
B.$ \dfrac{9}{2} $
C.$ \dfrac{7}{2} $
D.$ \dfrac{5}{2} $
答案:
B
3. 在横线上填上适当的数,使下列等式成立:
(1) $ x^{2}-2x + $______$ =(x - $______$)^{2} $;
(2) $ x^{2}+6x + $______$ =(x + $______$)^{2} $;
(3) $ x^{2}-9x + $______$ =(x - $______$)^{2} $;
(4) $ x^{2}+5x + $______$ =(x + $______$)^{2} $。
(1) $ x^{2}-2x + $______$ =(x - $______$)^{2} $;
(2) $ x^{2}+6x + $______$ =(x + $______$)^{2} $;
(3) $ x^{2}-9x + $______$ =(x - $______$)^{2} $;
(4) $ x^{2}+5x + $______$ =(x + $______$)^{2} $。
答案:
(1)1,1;
(2)9,3;
(3)$\frac{81}{4}$, $\frac{9}{2}$;
(4)$\frac{25}{4}$, $\frac{5}{2}$
(1)1,1;
(2)9,3;
(3)$\frac{81}{4}$, $\frac{9}{2}$;
(4)$\frac{25}{4}$, $\frac{5}{2}$
4. 若代数式 $ x^{2}-2x + b $ 可化为 $ (x + a)^{2}+2 $,则 $ a = $______,$ b = $______。
答案:
-1; 3
问题 求证:不论 $ x $ 取何值,代数式 $ 2x^{2}-4x + 14 $ 的值恒大于 $ 0 $。
名师指导
可以通过“配方”途径,从 $ 2x^{2}-4x + 14 $ 中“分离”出一个完全平方式,即将其变形为 $ a(x + b)^{2}+c $ 的形式。
解题示范(学生在教师指导下,独立完成)
证明:
]
名师指导
可以通过“配方”途径,从 $ 2x^{2}-4x + 14 $ 中“分离”出一个完全平方式,即将其变形为 $ a(x + b)^{2}+c $ 的形式。
解题示范(学生在教师指导下,独立完成)
证明:
]
答案:
证明:
$2x^{2}-4x + 14$
$=2(x^{2}-2x) + 14$
$=2(x^{2}-2x + 1 - 1) + 14$
$=2[(x - 1)^{2}-1] + 14$
$=2(x - 1)^{2}-2 + 14$
$=2(x - 1)^{2}+12$
$\because (x - 1)^{2} \geq 0$,
$\therefore 2(x - 1)^{2} \geq 0$,
$\therefore 2(x - 1)^{2}+12 \geq 12 > 0$。
即不论$x$取何值,代数式$2x^{2}-4x + 14$的值恒大于$0$。
$2x^{2}-4x + 14$
$=2(x^{2}-2x) + 14$
$=2(x^{2}-2x + 1 - 1) + 14$
$=2[(x - 1)^{2}-1] + 14$
$=2(x - 1)^{2}-2 + 14$
$=2(x - 1)^{2}+12$
$\because (x - 1)^{2} \geq 0$,
$\therefore 2(x - 1)^{2} \geq 0$,
$\therefore 2(x - 1)^{2}+12 \geq 12 > 0$。
即不论$x$取何值,代数式$2x^{2}-4x + 14$的值恒大于$0$。
1. 公元 9 世纪,阿拉伯数学家阿尔·花拉子米在解方程 $ x^{2}+2x = 35 $ 时采用的方法是:构造如图所示图形,一方面,正方形的面积为 $ (x + 1)^{2} $;另一方面,它又等于 $ 35 + 1 $,据此可得方程的一个正数解 $ x = 5 $。按照这种构造方法,我们在求方程 $ x^{2}+4x = 5 $ 的一个正数解时,可以构造如下图形 ( )

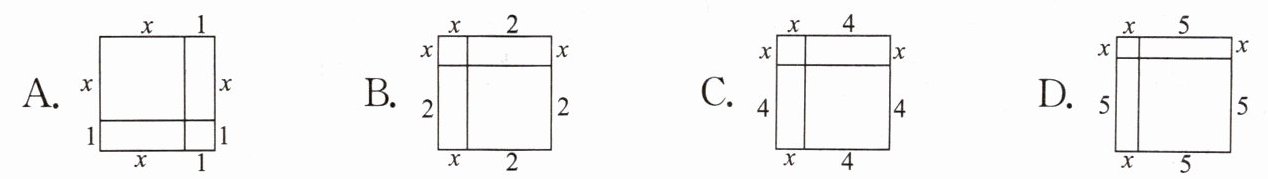
A.
B.
C.
D.]

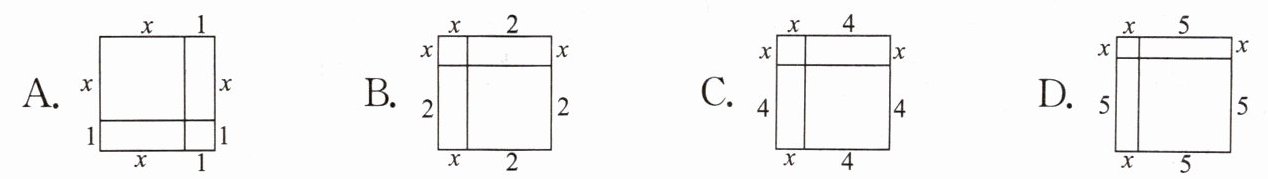
A.
B.
C.
D.]
答案:
B
查看更多完整答案,请扫码查看


