第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
1. 用一条长为40cm的绳子围成一个面积为$a cm^2$的长方形,a的值不可能为( )
A.20
B.40
C.100
D.120
A.20
B.40
C.100
D.120
答案:
D.
2. 已知△ABC中,∠A= 30°,AB+AC= 7,设AB= x,△ABC的面积为y,则y关于x的函数关系式为____.
答案:
$y=-\frac{1}{4}x^{2}+\frac{7}{4}x(0<x<7)$.
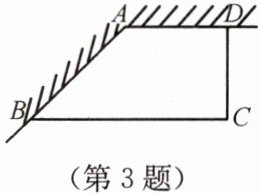
3. 如图,利用135°的墙角修建一个梯形的储料场(梯形ABCD),并使∠C= 90°.如果新建墙BCD总长15m,那么怎样修建才能使储料场的面积最大?

答案:
设$CD=x$,则$BC=15-x,AD=15-2x,S_{梯形ABCD}=\frac{1}{2}(30-3x)x=-\frac{3}{2}(x-5)^{2}+\frac{75}{2}$.当$CD=5$时,储料场的面积最大.
4. 【综合与实践】
项目主题:劳动基地扩建方案.
项目背景:学校计划扩建某劳动基地,综合实践活动小组以设计“劳动基地扩建方案”为主题开展了一次项目学习.
信息获取:
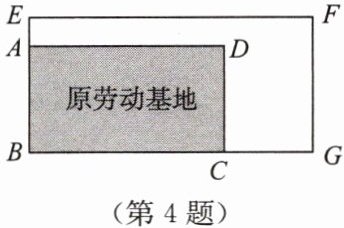
信息1,如图,原劳动基地为矩形,AB的长为25m,BC的长为45m;
信息2,如图,扩建后新劳动基地仍为矩形,BE的最大长度为32m,BG的最大长度为52m.
问题解决:
(1) 设该劳动基地两边增加相同的宽度x m,请直接写出新劳动基地的面积$y(m^2)$与x(m)的函数解析式.
(2) 在(1)的条件下,当新劳动基地的面积为$1500m^2$时,求BG和BE的长.
(3) 当CG= 3AE时,新劳动基地的面积可以为$1800m^2$吗? 请说明理由.
项目主题:劳动基地扩建方案.
项目背景:学校计划扩建某劳动基地,综合实践活动小组以设计“劳动基地扩建方案”为主题开展了一次项目学习.
信息获取:
信息1,如图,原劳动基地为矩形,AB的长为25m,BC的长为45m;
信息2,如图,扩建后新劳动基地仍为矩形,BE的最大长度为32m,BG的最大长度为52m.
问题解决:
(1) 设该劳动基地两边增加相同的宽度x m,请直接写出新劳动基地的面积$y(m^2)$与x(m)的函数解析式.
(2) 在(1)的条件下,当新劳动基地的面积为$1500m^2$时,求BG和BE的长.
(3) 当CG= 3AE时,新劳动基地的面积可以为$1800m^2$吗? 请说明理由.

答案:
(1)$y=x^{2}+70x+1125$;(2)$BE=30\ m,BG=50\ m$;(3)不可以,理由:假设扩建后的劳动基地的面积可以为$1800\ m^{2}$,设$AE=a\ m$,则$CG=3a\ m$,根据扩建后的劳动基地的面积为$1800\ m^{2}$,可列出关于$a$的一元二次方程,解之可得出$a=5$,将其代入$45+3a$中,可求出$45+3a=60$,由该值大于52,即可得出假设不成立,即当$CG=3AE$时,扩建后的劳动基地的面积不能为$1800\ m^{2}$.
某建筑的窗户如图所示,它的上半部是半圆,下半部是矩形.制造窗框的材料总长为15m(图中所有线条长度之和),当x等于多少时,窗户通过的光线最多? 此时,窗户的面积S是多少? (结果精确到0.01m)


答案:
由题意可知,$4y+\frac{1}{2}×2\pi x+7x=15$,化简得$y=\frac{15-7x-\pi x}{4}$,$S=\frac{1}{2}\pi x^{2}+2xy=-\frac{7}{2}x^{2}+\frac{15}{2}x$,当$x=\frac{15}{14}\approx1.07$时,$S_{最大值}=\frac{225}{56}\approx4.02$.
查看更多完整答案,请扫码查看


