第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
6. 下列命题:①各边相等的多边形是正多边形;②正多边形是中心对称图形;③正六边形的外接圆半径与边长相等;④正 $n$ 边形共有 $n$ 条对称轴.其中真命题有.(填序号)
答案:
③④.
7. 若一个正多边形的一个外角等于它的一个内角的 $\frac{1}{3}$,则这个正多边形是.
答案:
正八边形.
8. 如图,在正五边形 $ABCDE$ 中,$AC$ 与 $BE$ 相交于点 $F$,则 $\angle AFE$ 的度数为.
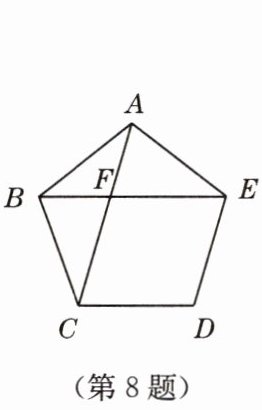

答案:
$72°$.
9. 2022 年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,将“雪花”图案(边长为 $4$ 的正六边形 $ABCDEF$)放在平面直角坐标系中,若 $AB$ 与 $x$ 轴垂直,顶点 $A$ 的坐标为 $(2,-3)$,则顶点 $C$ 的坐标为.
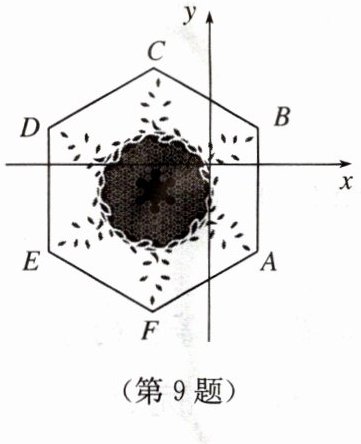

答案:
$(2-2\sqrt{3},3)$
10. 如图,小华从一个圆形场地点 $A$ 出发,沿着与半径 $OA$ 夹角为 $\alpha$ 的方向行走,走到场边缘 $B$ 后,再沿着与半径 $OB$ 夹角为 $\alpha$ 的方向折向行走,按照这种方式,小华第五次走到场地边缘时处于 $\overgroup{AB}$ 上,此时 $\angle AOE = 56^{\circ}$,则 $\alpha$ 的度数是 $^{\circ}$
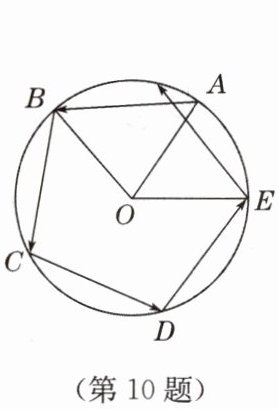

答案:
52.
11. 已知一个正三角形和一个正六边形的面积相等,则这两个正多边形的边长的比是.
答案:
$\sqrt{6}:1$.
如图,在正三角形 $ABC$ 中,$E$,$F$,$G$,$H$,$K$,$L$ 分别是各边的三等分点.
(1)求证:六边形 $EFGHKL$ 为正六边形;
(2)若 $AB = 3\mathrm{cm}$,求正六边形 $EFGHKL$ 的面积.
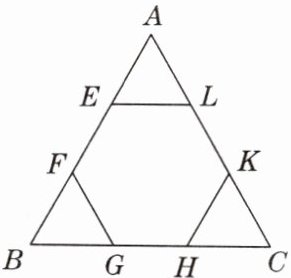
(1)求证:六边形 $EFGHKL$ 为正六边形;
(2)若 $AB = 3\mathrm{cm}$,求正六边形 $EFGHKL$ 的面积.

答案:
(1)提示:证六边形EFGHKL的6个内角相等,6条边相等;(2)$\frac{3\sqrt{3}}{2}\ cm^2$.
查看更多完整答案,请扫码查看


