《2025年新课程自主学习与测评九年级数学上册人教版》

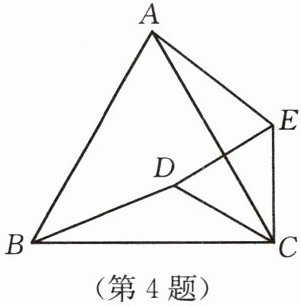
4. 如图,D为正△ABC内一点,将△BDC绕着点C旋转到△AEC的位置.
(1) △CDE是怎样的三角形？请说明理由.
(2) 通过(1),你发现△CDE的形状与哪一个角有关系？

答案： （1）$\triangle CDE$是等边三角形,理由略；（2）$\triangle CDE$的形状与$\angle ACB$有关,若$\angle ACB$是直角,则$\triangle CDE$是等腰直角三角形.

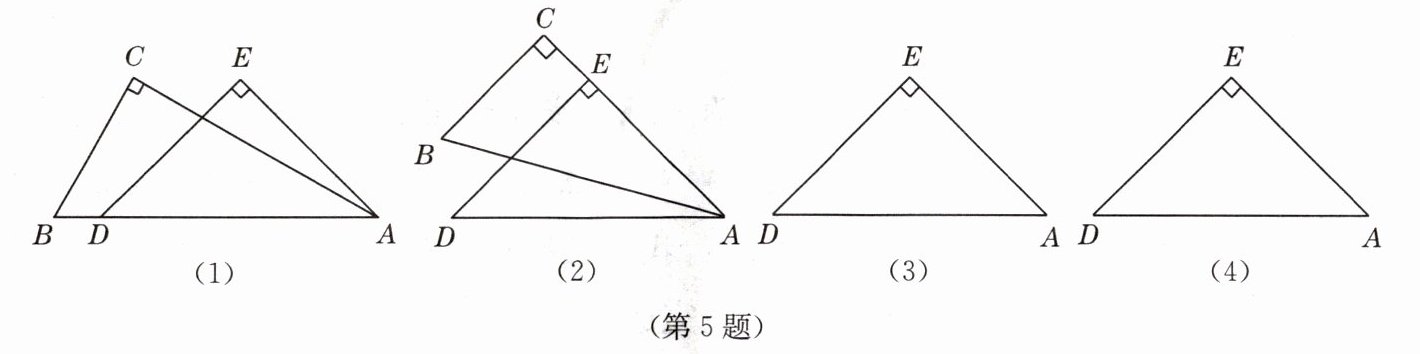
5. 一副直角三角板叠放如图(1)所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转∠α(∠α = ∠BAD且0° ＜ ∠α ＜ 180°),使两块三角板至少有一组边平行.
(1) 如图(2),∠α = ____°时,BC//DE.
(2) 请你分别在图(3)、(4)的指定框内,各画一种符合要求的图形,标出α,并完成各项填空：
图(3)中∠α = ____°时,____//____；
图(4)中∠α = ____°时,____//____.

答案： （1）15；（2）图略;60,$BC// AD$;105,$AC// DE$;135,$AB// DE$.（选填两种即可）

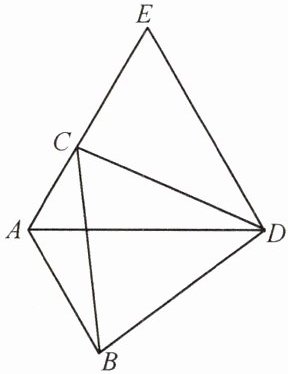
如图,在△ABC中,∠BAC = 120°,以BC为边向△ABC外作等边三角形BCD. 把△ABD绕着点D顺时针方向旋转60°后得到△ECD. 若AB = 3,AC = 2,求∠BAD的度数与AD的长.

答案： $\angle BAD=60°$,$AD=5$. 提示：可证明$\angle ACE=180°$,再证明$\triangle ADE$是等边三角形.

1. 若两个图形关于某点成中心对称,则以下说法中正确的是( )
① 这两个图形一定全等；② 对称点的连线一定经过对称中心；③ 一定存在某条直线,沿该直线折叠后的两个图形能互相重合.

A.①②
B.①③
C.②③
D.①②③

答案： A.