《2025年新课程自主学习与测评九年级数学上册人教版》

如图,菱形ABCD的边长为1.5 cm,B,C两点在扇形AEF的$\overgroup{EF}$上,求$\overgroup{BC}$的长度及扇形ABC的面积.

答案： $\overset{\frown}{BC}$ 的长度为 $\frac{\pi}{2}\, cm$；扇形 $ABC$ 的面积为 $\frac{3}{8}\pi\, cm^2$.

1. 已知矩形ABCD的一边AB为2 cm,另一边AD为4 cm,则以直线AD为轴旋转一周所得的图形是_________,其侧面积是_________$cm^2,$表面积是_________$cm^2.$

答案： 圆柱；$16\pi$；$24\pi$

2. 如图,有一圆柱,它的高为20 cm,底面半径为7 cm.在圆柱的下底面点A处有一只蜘蛛,它想吃到上底面上与点A相对的点B处的苍蝇,需要爬行的最短路径是______cm(结果用带根号和 $\pi$ 的式子表示).

答案： $\sqrt{49\pi^2 + 400}$

3. 如图是一个圆锥形冰激凌,已知它的母线长是13 cm,高是12 cm,则这个圆锥形冰激凌的底面面积是_________$cm^2.$
]

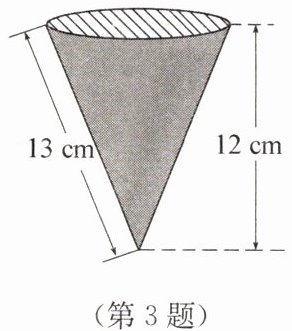
答案： $25\pi$

4. 如图,从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是______m.

答案： $\sqrt{30}$

5. 已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于_________$cm^2.$

答案： $24\pi$

问题 如图,圆锥的母线长为4,底面圆半径为1.若一只小虫从点A开始绕着圆锥表面爬行一圈到SA的中点C,试求小虫爬行的最短距离.

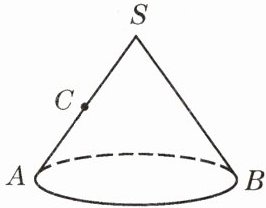
名师指导
直接求解无法看到小虫爬行的路线,只有将圆锥展开,在展开图上找到两点,利用两点之间线段最短进行求解.
解题示范(学生在教师指导下,独立完成)
解：

答案： 解：将圆锥侧面展开为扇形，设扇形圆心角为$n°$。
圆锥底面周长为$2\pi r = 2\pi × 1 = 2\pi$，展开后扇形弧长等于底面周长，扇形半径为母线长4。
由弧长公式$\frac{n\pi × 4}{180} = 2\pi$，解得$n = 90°$，即展开后扇形圆心角为$90°$。
展开图中，扇形顶点为$S$，半径$SA = SA' = 4$，$\angle ASA' = 90°$，$C$为$SA$中点，故$SC = \frac{4}{2} = 2$。
小虫爬行最短距离为展开图中$A'$与$C$的线段长（$A'$为扇形弧另一端点，卷成圆锥时与$A$重合）。
在$Rt\triangle SA'C$中，$SA' = 4$，$SC = 2$，则$A'C = \sqrt{SA'^2 + SC^2} = \sqrt{4^2 + 2^2} = \sqrt{20} = 2\sqrt{5}$。
答：小虫爬行的最短距离为$2\sqrt{5}$。