第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
1. 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED= 16m,AE= 8m,抛物线的顶点C到ED的距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1) 求抛物线的函数解析式;
(2) 已知从某时刻开始的40h内,水面与河底ED的距离h(m)随时间t(h)的变化满足函数关系h= -$\frac{1}{128}$(t-19)^2+8(0≤t≤40),且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?

(1) 求抛物线的函数解析式;
(2) 已知从某时刻开始的40h内,水面与河底ED的距离h(m)随时间t(h)的变化满足函数关系h= -$\frac{1}{128}$(t-19)^2+8(0≤t≤40),且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?

答案:
(1)$y=-\frac{3}{64}x^{2}+11$;(2)需32h禁止船只通行.
2. 【综合与实践】小东在复习二次函数时,遇到这样一个问题:
如图(1),一个横截面为抛物线形的公路隧道,其底部宽12m,最大高度6m.车辆双向通行,规定车辆必须在中心线两侧、距离道路边缘2m的范围内行驶,并保持车辆顶部与隧道有不少于$\frac{1}{3}$m的空隙.你能否根据这些要求,建立适当的平面直角坐标系,应用已有的函数知识,确定通过隧道车辆的高度限制?
如图(2),小东以点O为原点,地面OM所在的直线为x轴建立平面直角坐标系,请你帮小东解决问题:
2题
(1) 求出这条抛物线的函数解析式,并注明自变量x的取值范围;
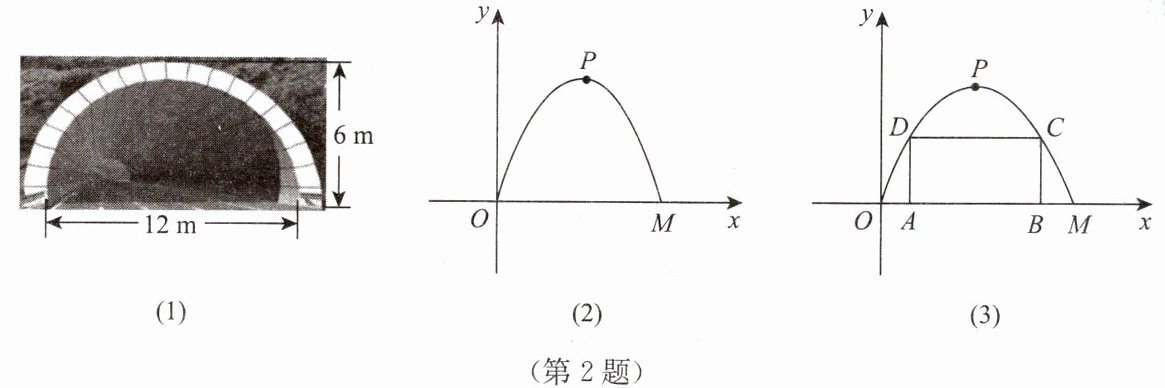
(2) 求出通过隧道车辆的高度限制应为多少米;
(3) 老师说:隧道检修过程中,计划搭建一个由矩形ABCD的三条边AD-DC-CB组成的“支撑架”,使C,D两点在抛物线上,A,B两点在地面OM上,如图(3).为了筹备材料,需求出这个“支撑架”三根木杆AD,DC,CB的长度之和的最大值是多少,请你帮忙计算一下.
如图(1),一个横截面为抛物线形的公路隧道,其底部宽12m,最大高度6m.车辆双向通行,规定车辆必须在中心线两侧、距离道路边缘2m的范围内行驶,并保持车辆顶部与隧道有不少于$\frac{1}{3}$m的空隙.你能否根据这些要求,建立适当的平面直角坐标系,应用已有的函数知识,确定通过隧道车辆的高度限制?
如图(2),小东以点O为原点,地面OM所在的直线为x轴建立平面直角坐标系,请你帮小东解决问题:
2题
(1) 求出这条抛物线的函数解析式,并注明自变量x的取值范围;

(2) 求出通过隧道车辆的高度限制应为多少米;
(3) 老师说:隧道检修过程中,计划搭建一个由矩形ABCD的三条边AD-DC-CB组成的“支撑架”,使C,D两点在抛物线上,A,B两点在地面OM上,如图(3).为了筹备材料,需求出这个“支撑架”三根木杆AD,DC,CB的长度之和的最大值是多少,请你帮忙计算一下.
答案:
(1)$y=-\frac{1}{6}(x-6)^{2}+6(0\leqslant x\leqslant12)$;(2)3米;(3)这个支架总长的最大值为15米.
查看更多完整答案,请扫码查看


