2025年全优课堂八年级数学下册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优课堂八年级数学下册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 如图,在Rt△ABC中,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.
(1) 猜想四边形AFDE是什么四边形并证明你的猜想;
(2)若AB=8,BC=10,求四边形AFDE的周长.
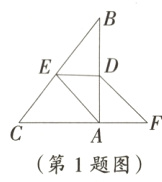
(1) 猜想四边形AFDE是什么四边形并证明你的猜想;
(2)若AB=8,BC=10,求四边形AFDE的周长.

答案:
解:
(1)四边形AFDE是平行四边形.证明:
∵D,E分别为AB,BC的中点,
∴DE//AC,DE = $\frac{1}{2}$AC,
∴AD = DB,CE = BE,
∵∠BAC = 90°,
∴∠BDE = ∠BAF = 90°,在△DFA和△BED中,$\begin{cases}\angle FDA = \angle B \\AD = DB \\\angle DAF = \angle BDE\end{cases}$,
∴△DFA≌△BED(ASA),AF = DE,又
∵DE//AC,
∴DE//AF,
∴四边形AFDE是平行四边形;
(2)
∵AB = 8,BC = 10,
∴AC = 6,
∴DE = 3,
∵E为BC的中点,
∴AE = $\frac{1}{2}$BC = 5,
∴四边形AFDE的周长 = 2DE + 2AE = 6 + 10 = 16.
(1)四边形AFDE是平行四边形.证明:
∵D,E分别为AB,BC的中点,
∴DE//AC,DE = $\frac{1}{2}$AC,
∴AD = DB,CE = BE,
∵∠BAC = 90°,
∴∠BDE = ∠BAF = 90°,在△DFA和△BED中,$\begin{cases}\angle FDA = \angle B \\AD = DB \\\angle DAF = \angle BDE\end{cases}$,
∴△DFA≌△BED(ASA),AF = DE,又
∵DE//AC,
∴DE//AF,
∴四边形AFDE是平行四边形;
(2)
∵AB = 8,BC = 10,
∴AC = 6,
∴DE = 3,
∵E为BC的中点,
∴AE = $\frac{1}{2}$BC = 5,
∴四边形AFDE的周长 = 2DE + 2AE = 6 + 10 = 16.
2. 小明遇到这样一个问题:如图1,在△ABC中,DE//BC分别交AB于点D,交AC于点E. 已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF//DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
(1)请回答:BC+DE的值为 __________;
(2)参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
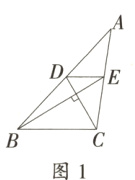
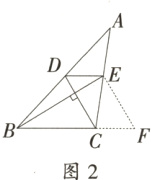
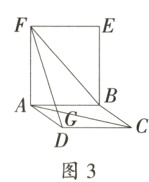
小明发现,过点E作EF//DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
(1)请回答:BC+DE的值为 __________;
(2)参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.



答案:
解:$\sqrt{34}$ 提示:
∵DE//BC,EF//DC,
∴四边形DCFE是平行四边形,
∴EF = CD = 3,CF = DE,
∵CD⊥BE,
∴EF⊥BE,
∴BC + DE = BC + CF = BF = $\sqrt{BE^{2}+EF^{2}}$ = $\sqrt{5^{2}+3^{2}}$ = $\sqrt{34}$;
(2)如图,连接AE,CE.
∵四边形ABCD是平行四边形,
∴AB//DC,AB = DC,
∵四边形ABEF是矩形,
∴AB//FE,AB = EF,BF = AE,
∴DC//EF,DC = EF,
∴四边形DCEF是平行四边形,
∴CE//DF,CE = DF,
∵AC = BF = DF,
∴AC = AE = CE,
∴△ACE是等边三角形,
∴∠ACE = 60°.
∵CE//DF,
∴∠AGF = ∠ACE = 60°.

解:$\sqrt{34}$ 提示:
∵DE//BC,EF//DC,
∴四边形DCFE是平行四边形,
∴EF = CD = 3,CF = DE,
∵CD⊥BE,
∴EF⊥BE,
∴BC + DE = BC + CF = BF = $\sqrt{BE^{2}+EF^{2}}$ = $\sqrt{5^{2}+3^{2}}$ = $\sqrt{34}$;
(2)如图,连接AE,CE.
∵四边形ABCD是平行四边形,
∴AB//DC,AB = DC,
∵四边形ABEF是矩形,
∴AB//FE,AB = EF,BF = AE,
∴DC//EF,DC = EF,
∴四边形DCEF是平行四边形,
∴CE//DF,CE = DF,
∵AC = BF = DF,
∴AC = AE = CE,
∴△ACE是等边三角形,
∴∠ACE = 60°.
∵CE//DF,
∴∠AGF = ∠ACE = 60°.

3. 如图,四边形ABCD是正方形,AB=4,E是边CD上的点,F是DA延长线上的点,且CE=AF,将△BCE沿BE折叠,得到△BC'E,延长BC'交AD于点G.
(1)求证:△BCE≌△BAF;
(2)①若DG=1,求FG的长;
②若∠CBE=30°,点B和点H关于DF的对称,求证:四边形FHGB是菱形.
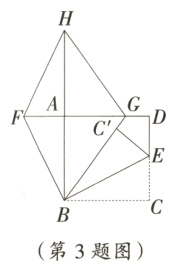
(1)求证:△BCE≌△BAF;
(2)①若DG=1,求FG的长;
②若∠CBE=30°,点B和点H关于DF的对称,求证:四边形FHGB是菱形.

答案:
解:
(1)证明:在正方形ABCD中,BC = BA,∠C = ∠BAD = ∠BAF = 90°,又
∵CE = AF,
∴△BCE≌△BAF(SAS);
(2)①
∵△BCE≌△BAF,
∴∠ABF = ∠CBE,
∵∠ABE + ∠CBE = 90°,
∴∠FBE = ∠ABE + ∠ABF = 90°,
∴∠FBG = 90° - ∠C'BE = 90° - ∠CBE = 90° - ∠ABF = ∠GFB,
∴FG = BG,
∵AD = AB = 4,DG = 1,
∴AG = 3,BG = $\sqrt{AB^{2}+AG^{2}}$ = 5,
∴FG = BG = 5;
②证明:
∵∠CBE = 30°,
∴∠ABF = ∠CBE = ∠ABG = 30°,
∵点B关于DA的对称点为点H,
∴BF = HF,GH = GB,∠ABF = ∠AHF = 30° = ∠ABG = ∠GHA,
∴BF//GH,FH//BG,
∴四边形FHGB是平行四边形,
∵BH⊥GF,
∴平行四边形FHGB是菱形.
(1)证明:在正方形ABCD中,BC = BA,∠C = ∠BAD = ∠BAF = 90°,又
∵CE = AF,
∴△BCE≌△BAF(SAS);
(2)①
∵△BCE≌△BAF,
∴∠ABF = ∠CBE,
∵∠ABE + ∠CBE = 90°,
∴∠FBE = ∠ABE + ∠ABF = 90°,
∴∠FBG = 90° - ∠C'BE = 90° - ∠CBE = 90° - ∠ABF = ∠GFB,
∴FG = BG,
∵AD = AB = 4,DG = 1,
∴AG = 3,BG = $\sqrt{AB^{2}+AG^{2}}$ = 5,
∴FG = BG = 5;
②证明:
∵∠CBE = 30°,
∴∠ABF = ∠CBE = ∠ABG = 30°,
∵点B关于DA的对称点为点H,
∴BF = HF,GH = GB,∠ABF = ∠AHF = 30° = ∠ABG = ∠GHA,
∴BF//GH,FH//BG,
∴四边形FHGB是平行四边形,
∵BH⊥GF,
∴平行四边形FHGB是菱形.
4. 如图,在四边形ABCD中,AD//BC,∠B=90°,AD=8 cm,BC=10 cm,AB=6 cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2 cm/s的速度向点C运动,P,Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s).
(1)直接写出:QD=______ cm,PC=________ cm;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?
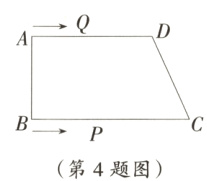
(1)直接写出:QD=______ cm,PC=________ cm;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?

答案:
解:
(1)(8 - t) (10 - 2t)
(2)
∵四边形PQDC是平行四边形,而AD//BC,
∴DQ = PC,由
(1),知DQ = 8 - t,PC = 10 - 2t,
∴8 - t = 10 - 2t,解得t = 2,即t = 2 s时,四边形PQDC是平行四边形;
(3)由
(1)
(2),知AQ = t,BP = 2t,DQ = 8 - t,PC = 10 - 2t,
∵△DPQ是等腰三角形,且DQ≠DP,
∴①当DP = QP时,点P在DQ的垂直平分线上,
∴AQ + $\frac{1}{2}$DQ = BP,
∴t + $\frac{1}{2}$(8 - t) = 2t,解得t = $\frac{8}{3}$;
②如图,当DQ = PQ时,过点Q作QE⊥BC于点E,则∠BEQ = ∠AQE = 90°,
∵AD//BC,∠B = 90°,
∴四边形ABEQ是矩形,
∴EQ = AB = 6,BE = AQ = t,
∴PE = BP - BE = t,在Rt△PEQ中,PQ = $\sqrt{PE^{2}+EQ^{2}}$ = $\sqrt{t^{2}+36}$,
∵DQ = 8 - t,
∴$\sqrt{t^{2}+36}$ = 8 - t,解得t = $\frac{7}{4}$,
∵点P在边BC上,不与点C重合,
∴0≤2t<10,
∴0≤t<5,
∴此种情况符合题意,
综上,当t = $\frac{8}{3}$ s或$\frac{7}{4}$ s时,△DPQ是等腰三角形.

解:
(1)(8 - t) (10 - 2t)
(2)
∵四边形PQDC是平行四边形,而AD//BC,
∴DQ = PC,由
(1),知DQ = 8 - t,PC = 10 - 2t,
∴8 - t = 10 - 2t,解得t = 2,即t = 2 s时,四边形PQDC是平行四边形;
(3)由
(1)
(2),知AQ = t,BP = 2t,DQ = 8 - t,PC = 10 - 2t,
∵△DPQ是等腰三角形,且DQ≠DP,
∴①当DP = QP时,点P在DQ的垂直平分线上,
∴AQ + $\frac{1}{2}$DQ = BP,
∴t + $\frac{1}{2}$(8 - t) = 2t,解得t = $\frac{8}{3}$;
②如图,当DQ = PQ时,过点Q作QE⊥BC于点E,则∠BEQ = ∠AQE = 90°,
∵AD//BC,∠B = 90°,
∴四边形ABEQ是矩形,
∴EQ = AB = 6,BE = AQ = t,
∴PE = BP - BE = t,在Rt△PEQ中,PQ = $\sqrt{PE^{2}+EQ^{2}}$ = $\sqrt{t^{2}+36}$,
∵DQ = 8 - t,
∴$\sqrt{t^{2}+36}$ = 8 - t,解得t = $\frac{7}{4}$,
∵点P在边BC上,不与点C重合,
∴0≤2t<10,
∴0≤t<5,
∴此种情况符合题意,
综上,当t = $\frac{8}{3}$ s或$\frac{7}{4}$ s时,△DPQ是等腰三角形.

查看更多完整答案,请扫码查看


