2025年全优课堂八年级数学下册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优课堂八年级数学下册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 以下是甲、乙两人证明$\sqrt{15}+\sqrt{8}\neq\sqrt{15 + 8}$的过程:
甲:因为$\sqrt{15}>\sqrt{9}=3$,$\sqrt{8}>\sqrt{4}=2$,所以$\sqrt{15}+\sqrt{8}>3 + 2 = 5$且$\sqrt{15 + 8}=\sqrt{23}<\sqrt{25}=5$,所以$\sqrt{15}+\sqrt{8}>5>\sqrt{15 + 8}$,故$\sqrt{15}+\sqrt{8}\neq\sqrt{15 + 8}$;
乙:作一个直角三角形,两直角边长分别为$\sqrt{15}$,$\sqrt{8}$,利用勾股定理$(\sqrt{15})^2+(\sqrt{8})^2=15 + 8$,得斜边长为$\sqrt{15 + 8}$,因为$\sqrt{15 + 8}$,$\sqrt{15}$,$\sqrt{8}$为此三角形的三边长,所以$\sqrt{15}+\sqrt{8}>\sqrt{15 + 8}$,故$\sqrt{15}+\sqrt{8}\neq\sqrt{15 + 8}$。
判断两人的证法可得( )
A. 两人都正确
B. 两人都错误
C. 甲正确,乙错误
D. 甲错误,乙正确
甲:因为$\sqrt{15}>\sqrt{9}=3$,$\sqrt{8}>\sqrt{4}=2$,所以$\sqrt{15}+\sqrt{8}>3 + 2 = 5$且$\sqrt{15 + 8}=\sqrt{23}<\sqrt{25}=5$,所以$\sqrt{15}+\sqrt{8}>5>\sqrt{15 + 8}$,故$\sqrt{15}+\sqrt{8}\neq\sqrt{15 + 8}$;
乙:作一个直角三角形,两直角边长分别为$\sqrt{15}$,$\sqrt{8}$,利用勾股定理$(\sqrt{15})^2+(\sqrt{8})^2=15 + 8$,得斜边长为$\sqrt{15 + 8}$,因为$\sqrt{15 + 8}$,$\sqrt{15}$,$\sqrt{8}$为此三角形的三边长,所以$\sqrt{15}+\sqrt{8}>\sqrt{15 + 8}$,故$\sqrt{15}+\sqrt{8}\neq\sqrt{15 + 8}$。
判断两人的证法可得( )
A. 两人都正确
B. 两人都错误
C. 甲正确,乙错误
D. 甲错误,乙正确
答案:
A 提示:甲的证明中说明$\sqrt{15}+\sqrt{8}$的值大于 5,并且证明$\sqrt{15 + 8}$小于5,一个大于5的值与一个小于5的值一定是不能相等的;乙的证明中利用了勾股定理,结合三角形的两边之和大于第三边得证.
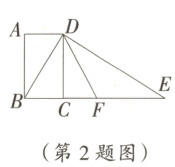
2. 如图,四边形$ABCD$为矩形,过点$D$作对角线$BD$的垂线,交$BC$的延长线于点$E$,取$BE$的中点$F$,连接$DF$,$DF = 4$。设$AB = x$,$AD = y$,则$x^2+(y - 4)^2$的值为( )
A. 4
B. $4\sqrt{2}$
C. 16
D. $16\sqrt{2}$

A. 4
B. $4\sqrt{2}$
C. 16
D. $16\sqrt{2}$
答案:
C 提示:
∵ 四边形 ABCD 是矩形,$AB = x,AD = y,\therefore CD = AB = x,BC = AD = y,\angle BCD = 90^{\circ}$.又$\because BD\perp DE$,点 F 是 BE 的中点,$DF = 4,\therefore BF = DF = EF = 4.\therefore CF = BF - BC = 4 - y$.
∴ 在$Rt\triangle DCF$中,$DC^{2}+CF^{2}=DF^{2}$,即$x^{2}+(4 - y)^{2}=4^{2}=16,\therefore x^{2}+(y - 4)^{2}=16$.
∵ 四边形 ABCD 是矩形,$AB = x,AD = y,\therefore CD = AB = x,BC = AD = y,\angle BCD = 90^{\circ}$.又$\because BD\perp DE$,点 F 是 BE 的中点,$DF = 4,\therefore BF = DF = EF = 4.\therefore CF = BF - BC = 4 - y$.
∴ 在$Rt\triangle DCF$中,$DC^{2}+CF^{2}=DF^{2}$,即$x^{2}+(4 - y)^{2}=4^{2}=16,\therefore x^{2}+(y - 4)^{2}=16$.
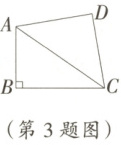
3. 如图,$\angle ABC = 90^{\circ}$,$AB = 6$,$BC = 8$,$AD = CD = 7$,若点$P$到$AC$的距离为$5$,则点$P$在四边形$ABCD$四条边上的个数为( )
A. 0
B. 2
C. 3
D. 4

A. 0
B. 2
C. 3
D. 4
答案:
A 提示:如图,过点 D 作$DE\perp AC$,垂足为点 E,过点 B 作$BF\perp AC$,垂足为点 F. 在$Rt\triangle ABC$中,$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10,\because AD = CD = 7,\therefore AE = CE=\frac{1}{2}AC = 5$.在$Rt\triangle ADE$中,$DE=\sqrt{AD^{2}-AE^{2}}=\sqrt{7^{2}-5^{2}}=2\sqrt{6}<5,\therefore AD$和 CD 边上不存在点 P;在$\triangle ABC$中,$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}AC\cdot BF$,即$AB\cdot BC = AC\cdot BF,BF=\frac{6\times8}{10}=4.8<5$,所以 AB 和 BC 边上也不存在点 P;综上,由于点 P 到AC 的距离为 5,则点 P 在四边形ABCD 四条边上的个数为 0.

A 提示:如图,过点 D 作$DE\perp AC$,垂足为点 E,过点 B 作$BF\perp AC$,垂足为点 F. 在$Rt\triangle ABC$中,$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10,\because AD = CD = 7,\therefore AE = CE=\frac{1}{2}AC = 5$.在$Rt\triangle ADE$中,$DE=\sqrt{AD^{2}-AE^{2}}=\sqrt{7^{2}-5^{2}}=2\sqrt{6}<5,\therefore AD$和 CD 边上不存在点 P;在$\triangle ABC$中,$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}AC\cdot BF$,即$AB\cdot BC = AC\cdot BF,BF=\frac{6\times8}{10}=4.8<5$,所以 AB 和 BC 边上也不存在点 P;综上,由于点 P 到AC 的距离为 5,则点 P 在四边形ABCD 四条边上的个数为 0.

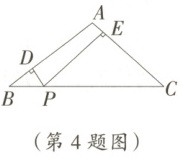
4. 如图,$\triangle ABC$中,$AB = AC = 5$,$BC = 8$,点$P$是$BC$边上的动点,过点$P$作$PD\perp AB$于点$D$,$PE\perp AC$于点$E$,则$PD + PE$的长是( )
A. 4.8
B. 4.8或3.8
C. 3.8
D. 5

A. 4.8
B. 4.8或3.8
C. 3.8
D. 5
答案:
A 提示:如图,过点 A 作$AF\perp BC$于点 F,连接 AP,$\because\triangle ABC$中,$AB = AC = 5,BC = 8,\therefore BF=\frac{1}{2}BC = 4,\therefore Rt\triangle ABF$中,$AF=\sqrt{AB^{2}-BF^{2}} = 3$,由图形,得$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,$\therefore\frac{1}{2}\times8\times3=\frac{1}{2}\times5\times PD+\frac{1}{2}\times5\times PE$,化简,得$12=\frac{5}{2}(PD + PE)$,解得$PD + PE = 4.8$.
5. 在探究矩形的性质时,小明得到了一个有趣的结论:矩形两条对角线长的平方和等于四条边长的平方和。如图1,在矩形$ABCD$中,由勾股定理,得$AC^2=AB^2+BC^2$,$BD^2=AB^2+AD^2$,又$CD = AB$,$AD = BC$,所以$AC^2+BD^2=AB^2+BC^2+CD^2+AD^2=2(AB^2+BC^2)$。
小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形的两条对角线长的平方和等于四条边长的平方和。请你解决下列问题:
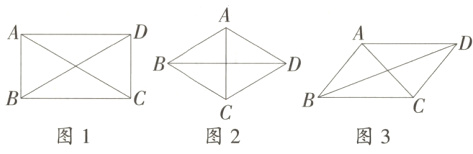
(1)如图2,已知:四边形$ABCD$是菱形,求证:$AC^2+BD^2=2(AB^2+BC^2)$;
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举例说明;
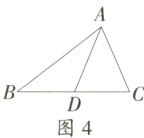
(3)如图4,在$\triangle ABC$中,$BC$,$AC$,$AB$的长分别为$a$,$b$,$c$,$AD$是$BC$边上的中线。试求$AD$的长。(结果用$a$,$b$,$c$表示)
小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形的两条对角线长的平方和等于四条边长的平方和。请你解决下列问题:

(1)如图2,已知:四边形$ABCD$是菱形,求证:$AC^2+BD^2=2(AB^2+BC^2)$;
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举例说明;
(3)如图4,在$\triangle ABC$中,$BC$,$AC$,$AB$的长分别为$a$,$b$,$c$,$AD$是$BC$边上的中线。试求$AD$的长。(结果用$a$,$b$,$c$表示)

答案:
解:
(1)证明:设 AC 与 BD 相交于点 O,
∵ 四边形 ABCD 是菱形,$\therefore AC\perp BD,AC = 2OA,BD = 2OB$.在$Rt\triangle AOB$中,由勾股定理,得$OA^{2}+OB^{2}=AB^{2}$,$\therefore AC^{2}+BD^{2}=4OA^{2}+4OB^{2}=4(OA^{2}+OB^{2})=4AB^{2}$,又$\because AB = BC$,$\therefore AC^{2}+BD^{2}=2(AB^{2}+AB^{2})=2(AB^{2}+BC^{2})$;
(2)小亮的猜想成立.证明:如图 1,作$AE\perp BC$于点 E,$DF\perp BC$交 BC 的延长线于点 F,则$\angle AEB=\angle DFC = 90^{\circ}$.$\because$四边形 ABCD 是平行四边形,$\therefore AB = DC,AB// CD,\therefore\angle ABE=\angle DCF$.$\therefore\triangle ABE\cong\triangle DCF,\therefore AE = DF,BE = CF$.在$Rt\triangle ACE$和$Rt\triangle BDF$中,由勾股定理,得$AC^{2}=AE^{2}+EC^{2}=AE^{2}+(BC - BE)^{2},BD^{2}=DF^{2}+BF^{2}=DF^{2}+(BC + CF)^{2}=AE^{2}+(BC + BE)^{2}$,$\therefore AC^{2}+BD^{2}=2AE^{2}+2BC^{2}+2BE^{2}=2(AE^{2}+BE^{2})+2BC^{2}$,又$AE^{2}+BE^{2}=AB^{2}$,故$AC^{2}+BD^{2}=2(AB^{2}+BC^{2})$;

(3)如图 2,延长 AD 到点 E,使$DE = AD$,连接 BE,CE,则$AE = 2AD$.$\because BD = CD,\therefore$四边形 ABEC 是平行四边形. 由
(2)的结论,得$AE^{2}+BC^{2}=2(AB^{2}+AC^{2})$,即$(2AD)^{2}+a^{2}=2(b^{2}+c^{2})$,解得$AD^{2}=\frac{1}{4}(2b^{2}+2c^{2}-a^{2})$,故$AD=\frac{1}{2}\sqrt{2b^{2}+2c^{2}-a^{2}}$.
解:
(1)证明:设 AC 与 BD 相交于点 O,
∵ 四边形 ABCD 是菱形,$\therefore AC\perp BD,AC = 2OA,BD = 2OB$.在$Rt\triangle AOB$中,由勾股定理,得$OA^{2}+OB^{2}=AB^{2}$,$\therefore AC^{2}+BD^{2}=4OA^{2}+4OB^{2}=4(OA^{2}+OB^{2})=4AB^{2}$,又$\because AB = BC$,$\therefore AC^{2}+BD^{2}=2(AB^{2}+AB^{2})=2(AB^{2}+BC^{2})$;
(2)小亮的猜想成立.证明:如图 1,作$AE\perp BC$于点 E,$DF\perp BC$交 BC 的延长线于点 F,则$\angle AEB=\angle DFC = 90^{\circ}$.$\because$四边形 ABCD 是平行四边形,$\therefore AB = DC,AB// CD,\therefore\angle ABE=\angle DCF$.$\therefore\triangle ABE\cong\triangle DCF,\therefore AE = DF,BE = CF$.在$Rt\triangle ACE$和$Rt\triangle BDF$中,由勾股定理,得$AC^{2}=AE^{2}+EC^{2}=AE^{2}+(BC - BE)^{2},BD^{2}=DF^{2}+BF^{2}=DF^{2}+(BC + CF)^{2}=AE^{2}+(BC + BE)^{2}$,$\therefore AC^{2}+BD^{2}=2AE^{2}+2BC^{2}+2BE^{2}=2(AE^{2}+BE^{2})+2BC^{2}$,又$AE^{2}+BE^{2}=AB^{2}$,故$AC^{2}+BD^{2}=2(AB^{2}+BC^{2})$;

(3)如图 2,延长 AD 到点 E,使$DE = AD$,连接 BE,CE,则$AE = 2AD$.$\because BD = CD,\therefore$四边形 ABEC 是平行四边形. 由
(2)的结论,得$AE^{2}+BC^{2}=2(AB^{2}+AC^{2})$,即$(2AD)^{2}+a^{2}=2(b^{2}+c^{2})$,解得$AD^{2}=\frac{1}{4}(2b^{2}+2c^{2}-a^{2})$,故$AD=\frac{1}{2}\sqrt{2b^{2}+2c^{2}-a^{2}}$.
查看更多完整答案,请扫码查看


