《2025年全优课堂八年级数学下册》

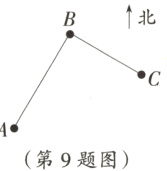
9. 如图，韩彬同学从家（记作A）出发向北偏东30°的方向行走了4 000 m到达超市（记作B），然后再从超市出发向南偏东60°的方向行走了3 000 m到达卢飞同学家（记作C），则韩彬家到卢飞家的距离为（ ）

A. 2 000 m
B. 3 000 m
C. 4 000 m
D. 5 000 m

答案： D 提示：在题图上连接AC.依题意，$∠ABC = 90^{\circ}$，$AB = 4000$m，$BC = 3000$m，则由勾股定理，得$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{4000^{2}+3000^{2}} = 5000(m)$．

10. 如图，一场大风后，一棵与地面垂直的树在离地面1 m处的A点折断，树尖B点触地，经测量BC = 3 m，那么树高是（ ）

A. 4 m
B. $\sqrt{10}$ m
C. ($\sqrt{10}$+1) m
D. ($\sqrt{10}$+3) m

答案： C 提示：由题意，知$AC = 1$m，$BC = 3$m，由勾股定理，得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{1^{2}+3^{2}}=\sqrt{10}(m)$，
∴ 树高为$AC + AB = (\sqrt{10}+1)m$．

11. 如图，已知楼梯的斜坡长为5 m，高为3 m，现计划在楼梯的表面铺地毯，则地毯的长度至少需要（ ）

A. 10 m
B. 9 m
C. 8 m
D. 7 m

答案： D 提示：由勾股定理，得楼梯的水平宽度$=\sqrt{5^{2}-3^{2}} = 4(m)$，
∵ 地毯铺满楼梯，
∴ 地毯的长度是楼梯的水平宽度与垂直高度的和，
∴ 地毯的长度至少是$3 + 4 = 7(m)$．

12. 如图所示，在数轴上点A所表示的数为a，则a的值为（ ）

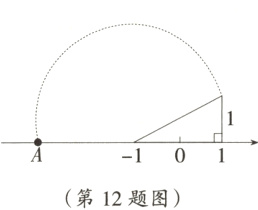
A. -1-$\sqrt{5}$
B. 1-$\sqrt{5}$
C. -$\sqrt{5}$
D. -1+$\sqrt{5}$

答案： A

13. 如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度为（滑轮上方部分忽略不计）（ ）

A. 12 m
B. 13 m
C. 16 m
D. 17 m

答案： D

14. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7 m，顶端距离地面2.4 m。如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2 m，则小巷的宽度为（ ）


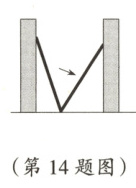
A. 0.7 m
B. 1.5 m
C. 2.2 m
D. 2.4 m

答案：
C 提示：如图，在Rt△ACB中，
∵$∠ACB = 90^{\circ}$，$BC = 0.7$m，$AC = 2.4$m，
∴$AB^{2}=0.7^{2}+2.4^{2}=6.25$．在Rt△A'BD中，
∵$∠A'DB = 90^{\circ}$，$A'D = 2$m，$BD^{2}+A'D^{2}=A'B^{2}=AB^{2}$，
∴$BD^{2}+2^{2}=6.25$，
∴$BD^{2}=2.25$．
∵$(\pm1.5)^{2}=2.25$，又
∵$BD＞0$，
∴$BD = 1.5$m，
∴$CD = BC + BD = 0.7+1.5 = 2.2(m)$．

15. 如图，在平静的湖面上，有一枝红莲BA，高出水面的部分AC为1 m，一阵风吹来，红莲被吹到一边，花朵齐及水面（即AB = DB），已知红莲移动的水平距离CD为3 m，则湖水深BC为（ ）


A. 12 m
B. 4 m
C. 3 m
D. $\sqrt{3}$ m

答案： B 提示：红莲被吹到一边，花朵刚好齐及水面，即$AB = BD$，均为红莲的长．在Rt△BCD中，设$BC = h$m，$AB = BD=(h + 1)$m，$DC = 3$m，由勾股定理，得$BD^{2}=DC^{2}+BC^{2}$，即$(h + 1)^{2}=3^{2}+h^{2}$，解得$h = 4$．

16. 如图，一菜农要修建一个育苗棚，棚宽BE = 2 m，棚高AE = 1.5 m，长BC = 18 m。AE所在的墙面与地面垂直，现要在棚顶覆盖一种农用塑料薄膜，则共需这种塑料薄膜______ $m^{2}$。

答案： 45

17. 如图，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉伸3 cm到D，则橡皮筋被拉长了______ cm。

答案： 2 提示：在Rt△ACD中，$AC=\frac{1}{2}AB = 4$cm，$CD = 3$cm，根据勾股定理，得$AD=\sqrt{AC^{2}+CD^{2}} = 5(cm)$，
∴$AD + BD - AB = 2AD - AB = 10 - 8 = 2(cm)$，故橡皮筋被拉长了2 cm．

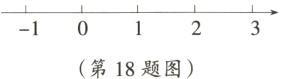
18. 在数轴上画出表示$\sqrt{3}$的点。

答案：
解：根据$1^{2}+(\sqrt{2})^{2}=(\sqrt{3})^{2}$作图，作图步骤：①作出表示$\sqrt{2}$的点：首先过表示1的点E作垂线，再截取$AE = 1$，然后连接OA，再以O为圆心，OA长为半径画弧，与原点右边的数轴的交点C为表示$\sqrt{2}$的点；②作出表示$\sqrt{3}$的点：过点C作$BC\perp OC$，在BC上截取$BC = 1$，连接OB，以O为圆心，OB长为半径画弧，与原点右边的数轴交于点D，则点D即为表示$\sqrt{3}$的点．如图所示．