第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
2. 概念:如果一个$n× n$矩阵(教材中表现为方格图)的每行、每列以及两条对角线的元素之和都相等,且这些元素都是从 1 到$n$的自然数,这样的矩阵就称为$n$阶幻方. 有关幻方问题的研究在我国已流传了两千多年,这是一类形式独特的填数字问题.
下面介绍一种构造三阶幻方的方法——杨辉法:口诀(如图)为“九子斜对,上下对易,左右相更,四维挺出”.
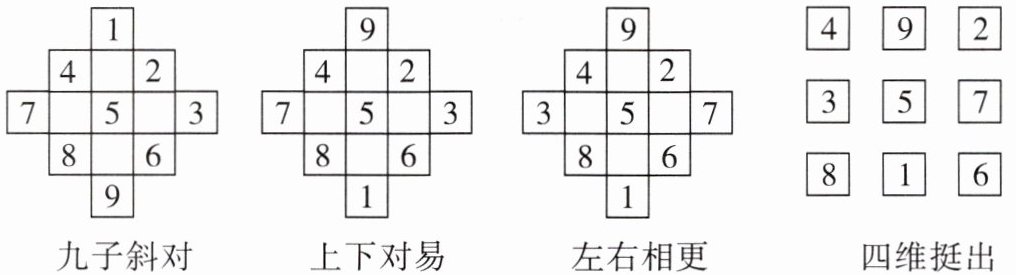
(1)请你将下列九个数:$-18$,$-16$,$-14$,$-12$,$-10$,$-8$,$-6$,$-4$,$-2$分别填入图①中的方格 1 中,使得每行、每列以及每条对角线上的三个数之和都相等;
(2)将图①方格 2 中的 9 个数填入方格 3 中,使每行、每列以及每条对角线上的三个数之和都相等;
(3)请你将下列九个数:4,6,8,$-5$,$-3$,$-1$,13,15,17 分别填入图①中的方格 4 中,使得每行、每列以及每条对角线上的三个数之和都相等;

(4)请将$-6$,$-3$,0,3,6,9,12,15,18 填入图②,使其构成一个幻方;
(5)如图③,在一个由 6 个圆圈组成的三角形里,把$-7$,$-6$,$-5$,$-4$,$-3$,$-2$这 6 个连续整数分别填入圆圈中,要求三角形的每条边上的三个数的和$S$都相等,请直接写出$S$的最大值.
下面介绍一种构造三阶幻方的方法——杨辉法:口诀(如图)为“九子斜对,上下对易,左右相更,四维挺出”.

(1)请你将下列九个数:$-18$,$-16$,$-14$,$-12$,$-10$,$-8$,$-6$,$-4$,$-2$分别填入图①中的方格 1 中,使得每行、每列以及每条对角线上的三个数之和都相等;
(2)将图①方格 2 中的 9 个数填入方格 3 中,使每行、每列以及每条对角线上的三个数之和都相等;
(3)请你将下列九个数:4,6,8,$-5$,$-3$,$-1$,13,15,17 分别填入图①中的方格 4 中,使得每行、每列以及每条对角线上的三个数之和都相等;

(4)请将$-6$,$-3$,0,3,6,9,12,15,18 填入图②,使其构成一个幻方;
(5)如图③,在一个由 6 个圆圈组成的三角形里,把$-7$,$-6$,$-5$,$-4$,$-3$,$-2$这 6 个连续整数分别填入圆圈中,要求三角形的每条边上的三个数的和$S$都相等,请直接写出$S$的最大值.
答案:
(1)
首先求这九个数的和$S=-18 - 16-14 - 12-10 - 8-6 - 4-2=\frac{(-18 - 2)×9}{2}=-90$,则每行、每列、每条对角线的和为$\frac{-90}{3}=-30$。
中间数为$-10$(因为三阶幻方中间数是这$9$个数的平均数)。
然后根据$-18+( - 2)+(-10)=-30$,$-16+( - 4)+(-10)=-30$,$-14+( - 6)+(-10)=-30$,$-12+( - 8)+(-10)=-30$,以及对角线和为$-30$,可得:
$\begin{bmatrix}-16&-18&-16\\-6&-10&-14\\-8&-12&-10\end{bmatrix}$(答案不唯一,可通过旋转、对称得到其他形式)。
(2)
$\begin{bmatrix}8&10&6\\6&8&10\\10&6&8\end{bmatrix}$
3. (3)
先求这九个数的和$S = 4 + 6+8-5 - 3-1 + 13+15+17=(4 + 6+8)+(-5 - 3-1)+(13+15+17)=18-9 + 45=54$,则每行、每列、每条对角线的和为$\frac{54}{3}=18$。
中间数为$6$(因为三阶幻方中间数是这$9$个数的平均数$\frac{54}{9}=6$)。
然后根据$4 + 17+(-3)=18$,$8 + 15+(-5)=18$,$13+6+(-1)=18$,$-5+6+17 = 18$等关系,可得:
$\begin{bmatrix}-5&17&6\\13&6&-1\\8&-3&13\end{bmatrix}$(答案不唯一,可通过旋转、对称得到其他形式)。
(4)
先求这九个数的和$S=-6 - 3+0 + 3+6+9+12+15+18=\frac{(-6 + 18)×9}{2}=54$,则每行、每列、每条对角线的和为$\frac{54}{3}=18$。
中间数为$6$(因为三阶幻方中间数是这$9$个数的平均数$\frac{54}{9}=6$)。
然后根据$-6+18 + 6=18$,$-3+15 + 6=18$,$0+12 + 6=18$,$3+9 + 6=18$,以及对角线和为$18$,可得:
$\begin{bmatrix}-3&18&3\\12&6&0\\9&-6&15\end{bmatrix}$(答案不唯一,可通过旋转、对称得到其他形式)。
(5)S的最大值为-12
首先求这九个数的和$S=-18 - 16-14 - 12-10 - 8-6 - 4-2=\frac{(-18 - 2)×9}{2}=-90$,则每行、每列、每条对角线的和为$\frac{-90}{3}=-30$。
中间数为$-10$(因为三阶幻方中间数是这$9$个数的平均数)。
然后根据$-18+( - 2)+(-10)=-30$,$-16+( - 4)+(-10)=-30$,$-14+( - 6)+(-10)=-30$,$-12+( - 8)+(-10)=-30$,以及对角线和为$-30$,可得:
$\begin{bmatrix}-16&-18&-16\\-6&-10&-14\\-8&-12&-10\end{bmatrix}$(答案不唯一,可通过旋转、对称得到其他形式)。
(2)
$\begin{bmatrix}8&10&6\\6&8&10\\10&6&8\end{bmatrix}$
3. (3)
先求这九个数的和$S = 4 + 6+8-5 - 3-1 + 13+15+17=(4 + 6+8)+(-5 - 3-1)+(13+15+17)=18-9 + 45=54$,则每行、每列、每条对角线的和为$\frac{54}{3}=18$。
中间数为$6$(因为三阶幻方中间数是这$9$个数的平均数$\frac{54}{9}=6$)。
然后根据$4 + 17+(-3)=18$,$8 + 15+(-5)=18$,$13+6+(-1)=18$,$-5+6+17 = 18$等关系,可得:
$\begin{bmatrix}-5&17&6\\13&6&-1\\8&-3&13\end{bmatrix}$(答案不唯一,可通过旋转、对称得到其他形式)。
(4)
先求这九个数的和$S=-6 - 3+0 + 3+6+9+12+15+18=\frac{(-6 + 18)×9}{2}=54$,则每行、每列、每条对角线的和为$\frac{54}{3}=18$。
中间数为$6$(因为三阶幻方中间数是这$9$个数的平均数$\frac{54}{9}=6$)。
然后根据$-6+18 + 6=18$,$-3+15 + 6=18$,$0+12 + 6=18$,$3+9 + 6=18$,以及对角线和为$18$,可得:
$\begin{bmatrix}-3&18&3\\12&6&0\\9&-6&15\end{bmatrix}$(答案不唯一,可通过旋转、对称得到其他形式)。
(5)S的最大值为-12
查看更多完整答案,请扫码查看


