《2025年全效学习学业评价方案七年级数学上册人教版》

10. [2024 邵东模拟]如图，数轴上有 $A$，$B$，$C$，$D$ 四个点，其中绝对值最小的数对应的点是（ ）


A.点 $A$
B.点 $B$
C.点 $C$
D.点 $D$

答案： 10.B

11. [2025 张家界模拟]已知有五个有理数，分别是：$-3$，$-(-4.5)$，$\vert -\frac{3}{2}\vert$，$2$，$-1$。
(1) 请把这五个有理数在图中的数轴上表示出来；
(2) 用“$＜$”把这五个有理数连接起来。
]

答案： 对于$-(-4.5)$，根据负负得正，可得$-(-4.5)=4.5$；
对于$\vert-\frac{3}{2}\vert$，根据绝对值的性质$\vert a\vert=\begin{cases}a(a\geq0)\\ -a(a\lt0)\end{cases}$，可得$\vert-\frac{3}{2}\vert=\frac{3}{2}=1.5$。
$ (2)-3 ＜ -1 ＜ -\frac{3}{2} ＜ 2 ＜ -(-4.5)$

12. 比较下列有理数的大小：
(1) $-\frac{4}{5}$ 与 $-\frac{5}{4}$；
(2) $-\frac{3}{4}$ 与 $-\frac{4}{5}$；
(3) $0$ 与 $-\vert -100\vert$；
(4) $2\frac{1}{2}$ 与 $\vert -2.5\vert$。

答案： $12.(1)-\frac{4}{5} ＞ -\frac{5}{4} (2)-\frac{3}{4} ＞ -\frac{4}{5} (3)0 ＞ -$|-100|$ (4)2\frac{1}{2} = $|-2.5|

13. [2024 北京模拟]如图，$A$，$B$ 分别为数轴上的两点，点 $A$ 所表示的数为 $-20$，点 $B$ 所表示的数为 $100$。

(1) 与 $A$，$B$ 两点距离相等的点 $M$ 所表示的数为________。
(2) 现有一只电子蚂蚁 $P$ 从点 $B$ 出发，以 $6$ 个单位长度/s 的速度向左运动；同时另一只电子蚂蚁 $Q$ 恰好从点 $A$ 出发，以 $4$ 个单位长度/s 的速度向右运动。设两只电子蚂蚁在数轴上的点 $C$ 相遇，则点 $C$ 所表示的数是________。
(3) 若当电子蚂蚁 $P$ 从点 $B$ 出发时，以 $6$ 个单位长度/s 的速度向左运动，同时另一只电子蚂蚁 $Q$ 恰好从点 $A$ 出发，以 $4$ 个单位长度/s 的速度也向左运动。请问：当它们运动时间是多少秒时，两只蚂蚁之间的距离为 $20$ 个单位长度？

答案： 13.
(1)40
(2)28
(3)当它们运动时间为50s或70s时，两只蚂蚁之间的距离为20个单位长度.

14. 【创新意识】[新趋势·数学文化]中国古代数学著作《九章算术》的“方程”一章中首次正式引入了负数。在生活中，我们规定 $(\uparrow 100)$ 元表示收入 $100$ 元，那么 $(\downarrow 80)$ 元表示（ ）

A.支出 $80$ 元
B.收入 $20$ 元
C.支出 $20$ 元
D.收入 $80$ 元

答案： 14.A

15. 【创新意识】[新趋势·学科融合]观察元素原子结构示意图的规律，则某元素原子结构的原子核中应填的是（ ）


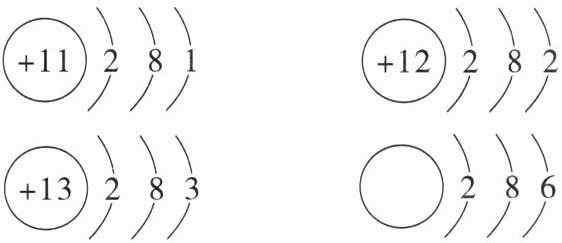
A.$+14$
B.$+15$
C.$+16$
D.$+18$

答案： 15.C