《2025年全效学习学业评价方案七年级数学上册人教版》

1. 如果 $ \angle A = 76^{\circ} $，$ \angle B = 104^{\circ} $，那么 $ \angle A $ 是 $ \angle B $ 的（ ）

A.直角
B.余角
C.补角
D.平角

答案： 1.C

2. 已知 $ \angle \alpha = 34^{\circ}30' $，则它的余角的度数为（ ）

A.$ 34^{\circ}30' $
B.$ 55^{\circ}30' $
C.$ 145^{\circ}30' $
D.$ 155^{\circ}30 $

答案： 2.B

3. （1）若 $ \angle \alpha = 35^{\circ} $，则 $ \angle \alpha $ 的补角的度数为______，$ \angle \alpha $ 的余角的度数为______，$ \angle \alpha $ 的补角与余角的度数差为______；
（2）若一个角是 $ 70^{\circ}39' $，则它的余角的度数是______。

答案： 3.
(1)145° 55° 90°
(2)19°21′

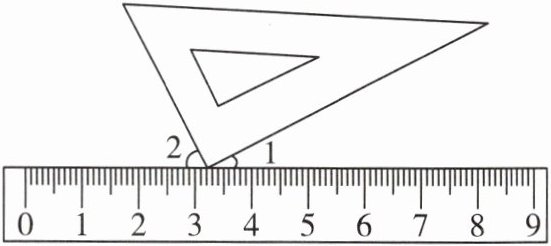
4. [2023 赣州模拟]按如图所示放置三角尺和直尺。
（1）$ \angle 1 $ 与 $ \angle 2 $ 的数量关系是______。
（2）若 $ \angle 1 $ 的补角比 $ \angle 2 $ 的 2 倍多 $ 25^{\circ} $，求 $ \angle 1 $ 的度数。

答案： 4.
(1)∠1＋∠2＝90°
(2)∠1的度数是25°

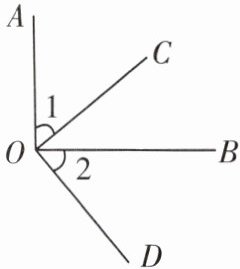
5. 如图，如果 $ \angle AOB = \angle COD = 90^{\circ} $，那么 $ \angle 1 = \angle 2 $，这是根据（ ）

A.直角都相等
B.等角的余角相等
C.同角的余角相等
D.同角的补角相等

答案： 5.C

6. 若 $ \angle \alpha = \angle \beta $，且 $ \angle \alpha + \angle 1 = 180^{\circ} $，$ \angle \beta + \angle 2 = 180^{\circ} $，则 $ \angle 1 $ 与 $ \angle 2 $ 的大小关系是______，理由是______。

答案： 6.∠1＝∠2 等角的补角相等

7. 如图，$ \angle AOB = \angle COD = 90^{\circ} $。
（1）$ \angle AOC $ 与 $ \angle BOD $ 相等吗？请说明理由。
（2）若 $ \angle BOD = 140^{\circ} $，射线 $ OE $ 平分 $ \angle AOC $，则 $ \angle DOE $ 的度数为______。

答案： 1. （1）
解：$\angle AOC$与$\angle BOD$相等。
理由：因为$\angle AOB=\angle COD = 90^{\circ}$，$\angle AOC+\angle AOD=\angle COD = 90^{\circ}$，$\angle BOD+\angle AOD=\angle AOB = 90^{\circ}$。
根据同角的余角相等，所以$\angle AOC=\angle BOD$。
2. （2）
因为$\angle BOD = 140^{\circ}$，$\angle AOC=\angle BOD$，所以$\angle AOC = 140^{\circ}$。
又因为射线$OE$平分$\angle AOC$，所以$\angle EOC=\frac{1}{2}\angle AOC$（角平分线定义），则$\angle EOC=\frac{1}{2}×140^{\circ}=70^{\circ}$。
因为$\angle COD = 90^{\circ}$，根据$\angle DOE=\angle COD-\angle EOC$。
所以$\angle DOE=90^{\circ}-70^{\circ}=20^{\circ}$。
故答案为$20^{\circ}$。

8. 下列说法正确的有______（填序号）。
①钝角与锐角互补；
② $ \angle \alpha $ 的余角是 $ 90^{\circ} - \angle \alpha $；
③ $ \angle \beta (0^{\circ} ＜ \angle \beta ＜ 180^{\circ}) $ 的补角是 $ 180^{\circ} - \angle \beta $；
④若 $ \angle 1 + \angle 2 + \angle 3 = 90^{\circ} $，则 $ \angle 1 $，$ \angle 2 $，$ \angle 3 $ 互余。

答案： 8.③

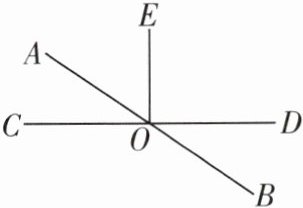
9. 如图，直线 $ AB $ 与 $ CD $ 相交于点 $ O $，且 $ \angle COE = 90^{\circ} $，则与 $ \angle EOA $ 互余的角有______。

答案： 9.∠COA,∠DOB