第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
7. (★) 如图, $ AD $ 与 $ BC $ 交于点 $ O $, $ \triangle ABO $ 和 $ \triangle CDO $ 关于直线 $ PQ $ 对称,点 $ A $, $ B $ 的对称点分别是点 $ C $, $ D $. 下列结论不一定正确的是 【

A.$ AD \perp BC $
B.$ AC \perp PQ $
C.$ \triangle ABO \cong \triangle CDO $
D.$ AC // BD $
]
A
】
A.$ AD \perp BC $
B.$ AC \perp PQ $
C.$ \triangle ABO \cong \triangle CDO $
D.$ AC // BD $
]
答案:
A
8. (★) 如图,五边形 $ ABCDE $ 是轴对称图形,直线 $ l $ 是其对称轴,已知四边形 $ ABCO $ 的周长为 $ 11 $, $ OA = 4 $,则五边形 $ ABCDE $ 的周长为

14
.
答案:
14
9. (★) (2024·滨州) 数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡儿心形线”. 其中不是轴对称图形的是 【
]

B
】]

答案:
B
10. (★★) (2024·甘肃) 围棋起源于中国,古代称为“弈”. 如图是两名同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点
]

A或C
的位置,则所得的对弈图是轴对称图形. (填写 $ A $, $ B $, $ C $, $ D $ 中的一处即可, $ A $, $ B $, $ C $, $ D $ 位于棋盘的格点上)]

答案:
A或C
11. (★) 如图,若 $ \triangle ABC $ 与 $ \triangle A_1B_1C_1 $ 关于直线 $ MN $ 对称, $ BB_1 $ 交 $ MN $ 于点 $ O $,则下列说法不一定正确的是 【
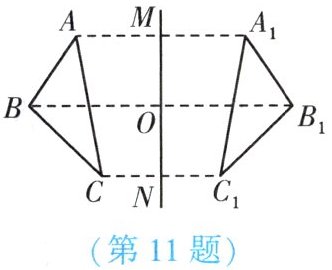
A.$ AC = A_1C_1 $
B.$ BO = B_1O $
C.$ CC_1 \perp MN $
D.$ AB // B_1C_1 $
]
D
】
A.$ AC = A_1C_1 $
B.$ BO = B_1O $
C.$ CC_1 \perp MN $
D.$ AB // B_1C_1 $
]
答案:
D
12. (★★) 如图,在 $ \triangle ABC $ 中, $ D $, $ E $, $ F $ 三点分别在 $ AB $, $ BC $, $ AC $ 上,且四边形 $ BEFD $ 是以 $ DE $ 所在直线为对称轴的轴对称图形,四边形 $ CFDE $ 是以 $ FE $ 所在直线为对称轴的轴对称图形. 若 $ \angle C = 40^{\circ} $,则 $ \angle DFE $ 的度数为
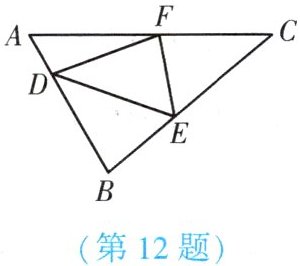
80°
.
答案:
80°
13. (★★) 如图,在 $ \triangle ABC $ 中, $ \angle CAB = 36^{\circ} $, $ \angle B = 48^{\circ} $, $ AB = 9 $, $ AC = 7 $, $ BC = 5.4 $, $ D $, $ E $ 分别是边 $ AB $ 和 $ BC $ 上的点,若 $ \triangle ACE $ 和 $ \triangle ADE $ 关于直线 $ AE $ 对称, $ CD $ 交 $ AE $ 于点 $ F $,则 $ \angle ADC $ 的度数为
]
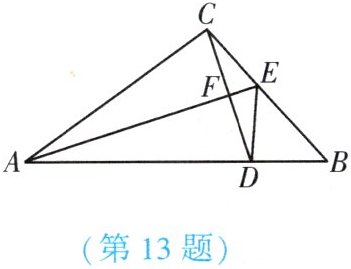
72°
, $ \triangle BDE $ 的周长为7.4
.]

答案:
72° 7.4
14.(★★★)如图,在3x3的正方形网格中,网格线的交点称为格点.以格点为顶点的三角形称为格点三角形,如△ABC为格点三角形,与△ABC成轴对称的格点三角形可以画出

A. 3 个
B. 4 个
C. 5 个
D. 6 个
答案:
D 提示:如图,与△ABC成轴对称的格点三角形A'B'C'可以画出6个.
D 提示:如图,与△ABC成轴对称的格点三角形A'B'C'可以画出6个.

查看更多完整答案,请扫码查看


