《2025年基础训练大象出版社八年级数学上册人教版》

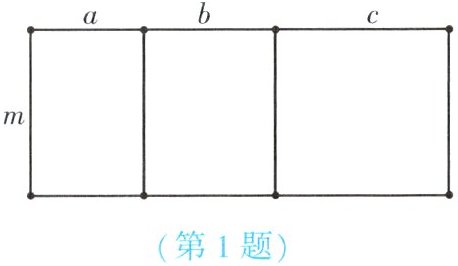
1. (★)如图,有一个边长为 $ m $ 的三个小长方形拼在一起组成新的长方形,则新长方形的面积可以表示为 $ m(a + b + c) $,也可以表示为ma+mb+mc,所以 $ m(a + b + c) = $ma+mb+mc。这个等式提供了单项式与多项式相乘的方法。

答案： ma+mb+mc ma+mb+mc

2. (★)一般地,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。

答案： 多项式的每一项 相加

3. (★)计算：$ 2a(3a - 2b) = $6a²-4ab；$ -x(x^{2} + x - 1) = $-x³-x²+x。

答案： 6a²-4ab -x³-x²+x

4. (★)计算$ -2x(x^{2} - y) $正确的是 【D】
A.$ -2x^{3} - y $
B.$ -2x^{3} - 2xy $
C.$ 2x^{3} - 2xy $
D.$ -2x^{3} + 2xy $

答案： D

5. (★)下列计算错误的是 【B】
A.$ 2x^{2}(\frac{1}{3}x - y) = \frac{2}{3}x^{3} - 2x^{2}y $
B.$ 3x^{2}y(1 - 2y^{3}) = 3x^{2}y + 6x^{2}y^{3} $
C.$ 2x(3x^{2} - xy + y) = 6x^{3} - 2x^{2}y + 2xy $
D.$ -2x(x^{2} - \frac{1}{2}x + 1) = -2x^{3} + x^{2} - 2x $

答案： B

6. (★)数学课上,老师讲了单项式乘多项式。放学回到家,小刚拿出课堂笔记复习,发现一道题：$ -4xy(3y - 2x - 3) = -12xy^{2}□ + 12xy $,$□$的地方被墨水弄污了。你认为$□$内应填写 【A】
A.$ +8x^{2}y $
B.$ -8x^{2}y $
C.$ +8xy $
D.$ -8xy^{2} $

答案： A

7. (★★)一个长方体的长为 $ 3x + 1 $,宽为 $ 2x $,高为 $ 3x $,则它的表面积为42x²+10x。

答案： 42x²+10x

8. (★★)计算：
(1) $ (2xy^{2} - 3xy) \cdot 2xy $；
(2) $ -2ab(ab - 3ab^{2} - 1) $；
(3) $ (\frac{3}{4}a^{n + 1} - \frac{b}{2}) \cdot ab $。

答案：
(1)4x²y³-6x²y²；
(2)-2a²b²+6a²b³+2ab；
(3)$\frac{3}{4}a^{n+2}b-\frac{1}{2}ab^{2}$.

9. (★★)求值：$ (a^{2}b + ab^{2} - 3b^{2}) \cdot 4ab^{2} - (-2ab^{2})^{2} $,其中 $ a = 2 $,$ b = \frac{1}{2} $。

答案： 原式=a²b·4ab²+ab·4ab²-3b²·4ab²-4a²b⁴=4a³b³+4a²b⁴-12ab⁴-4a²b⁴=4a³b³-12ab⁴.当a=2,b=$\frac{1}{2}$时,原式=4×(ab)³-12ab·b³=4×$(2×\frac{1}{2})^{3}$-12×$(2×\frac{1}{2})$×$(\frac{1}{2})^{3}$=4-12×$\frac{1}{8}$=$\frac{5}{2}$.